Задача B. Дерево Штерна-Броко ≡
| Автор: | Штерн, Броко, Ларькина | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 256 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 60 |
Условие
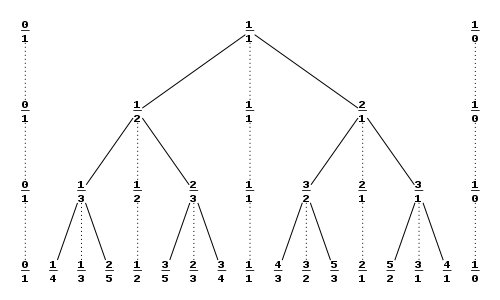
Один из способов построения множества всех неотрицательных несократимых дробей вида m/n называется деревом Штерна-Броко.
Начнем с дробей 0/1 и 1/0, а затем будем повторять следующую операцию: вставить дробь (m + m′)/(n + n′) между двумя соседними дробями m/n и m′/n′.
Например первый шаг дает одну новую дробь между 0/1 и 1/0: 0/1, 1/1, 1/0. Следующий шаг добавляет две дроби, получая 0/1, 1/2, 1/1, 2/1, 1/0. Весь процесс можно представить в виде бесконечного бинарного дерева (см. рисунок).
Воспользуемся символами L и R для обозначения левой и правой ветвей при продвижении от корня вниз к определенной дроби. Тогда строка символов L и R однозначно определяет местоположения дроби в дереве. Например, строка LRRL соответствует дроби 5/7.
Формат входного файла
Входной файл содержит два целых числа m n — числитель и знаменатель несократимой дроби соответственно.
Формат выходного файла
Выходной файл должен содержать строку, являющаяся представлением дроби в дереве Штерна-Броко.
Ограничения
1 ≤ N, M ≤ 105; N ≠ M
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 |
|
|