Problem G. Giant snake ≡
| Author: | I. Tuphanov | Time limit: | 1 sec | |
| Input file: | input.txt | Memory limit: | 256 Mb | |
| Output file: | output.txt |
Statement
Let us consider a snake consisting of L squares 1 × 1 meter in size,
chained one after another by sides.
There is a labyrinth of N × M cells. Each cell is 2 × 2 meters in size. Some cells are occupied by walls, others are empty.
Your task is to lay out the snake in the labyrinth without intersections with itself and walls, or determine that it is impossible.
Input file format
First line of input file contains three integers N M L. Following N lines consist of M characters each, describing the labyrinth. Free cells are denoted by '.' (ASCII 46). Walls are denoted by '#' (ASCII 35).Output file format
First line of output file must contain string YES if it is possible to lay out the snake and NO otherwise.
If the layout exists, the following L lines must contain positions of snake squares, listed in order they compose the snake. Each position is described by two integers ri ci, where ri is the distance from the top edge of the labyrinth to the top edge of the i-th square, (so 0 ≤ ri < 2 N), and ci is the distance form the left edge of the labyrinth to the left edge of the i-th square, (so 0 ≤ ci < 2 M).
If there is more than one layout, output any of them.
Constraints
1 ≤ N, M ≤ 50; 1 ≤ L ≤ 10000;Sample tests
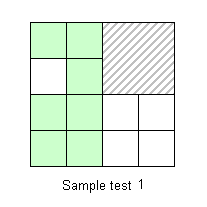
| No. | Input file (input.txt) |
Output file (output.txt) |
|---|---|---|
| 1 |
|
|