Задача 02B. Distribution by desks ≡
| Автор: | Евгений Татаринов, Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
Для проведения олимпиады по математике для 8−11 классов выделили несколько кабинетов. В первом кабинете стоит n рядов из парт, в каждом ряду по 3 парты, за одной партой может сидеть ровно один человек.
Организаторы олимпиады хотят посадить учеников за все парты первого кабинета так, что в любом квадрате из парт со стороной 2 будут сидеть ученики попарно разных классов (то есть, в любом квадрате сидит по одному ученику из 8-го, 9-го, 10-го и 11-го классов).
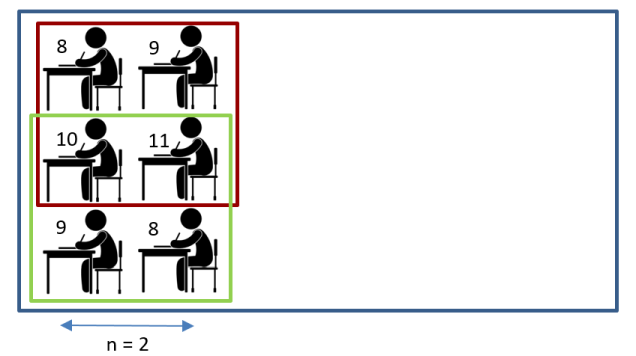
На рисунке вы можете видеть один из вариантов подходящей рассадки при n=2 (и в красном, и в зелёном квадратах все ученики из разных параллелей).
Сколько существует различных способов рассадки участников, если известно, что общее количество ребят любого класса больше, чем количество парт в первом кабинете?
Формат входных данных
Единственная строка входных данных содержит натуральное число n.
Формат выходных данных
Выведите одно натуральное число — ответ на вопрос задачи по модулю 109+7 (так как число может быть очень большим).
Ограничения
1≤n≤1018
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|