Задача B. Плавающие интерфейсы VR ≡
| Автор: | Dmitriy Merzlyakov | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 10 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 100 |
Условие

Юный программист Руслан занимается разработкой приложения виртуальной реальности, и, как в любом хорошем VR приложении, он хочет добавить пользовательский интерфейс, который бы плавно следовал за поворотом головы. Игрок находится внутри некоторой сферы S: x2 + y2 + z2 = R2. В начальный момент времени голова Игрока имеет координаты (xp0, yp0, zp0), взгляд исходит из центра головы и имеет направление l⃗ = (xd0, yd0, zd0), заданное вектором единичной длины.
Пользовательский интерфейс представляет собой пространственный прямоугольник шириной w и высотой h. Его центр в начальный момент времени совпадает с точкой пересечения луча, выходящего из центра головы по направлению l⃗, и сферы S.
 |
 |
В любой момент времени центр пользовательского интерфейса находится на поверхности сферы, а сам прямоугольник расположен в касательной плоскости к сфере S, таким образом, что его верхняя сторона всегда параллельна плоскости пола Oxy. Далее, игрок начинает произвольным образом двигаться и вращать головой так, что она не выходит за границы сферы.
Вам известна информация о положении головы (xpf, ypf, zpf) и направлении взгляда (xdf, ydf, zdf) для каждого кадра f = 1, 2, .... Если в какой-то кадр fi − 1 точка пересечения взгляда и плоскости пользовательского интерфейса находится внутри или на границе прямоугольника, а в следующем кадре fi – за его границей, то происходит запуск начала отсчёта задержки перед движением интерфейса в новое положение, которое составляет k кадров, начиная с fi. Если до завершения отсчёта точка пересечения взгляда и плоскости пользовательского интерфейса вернулась в границы прямоугольника, то отсчёт сбрасывается, и процедура ожидания повторяется.
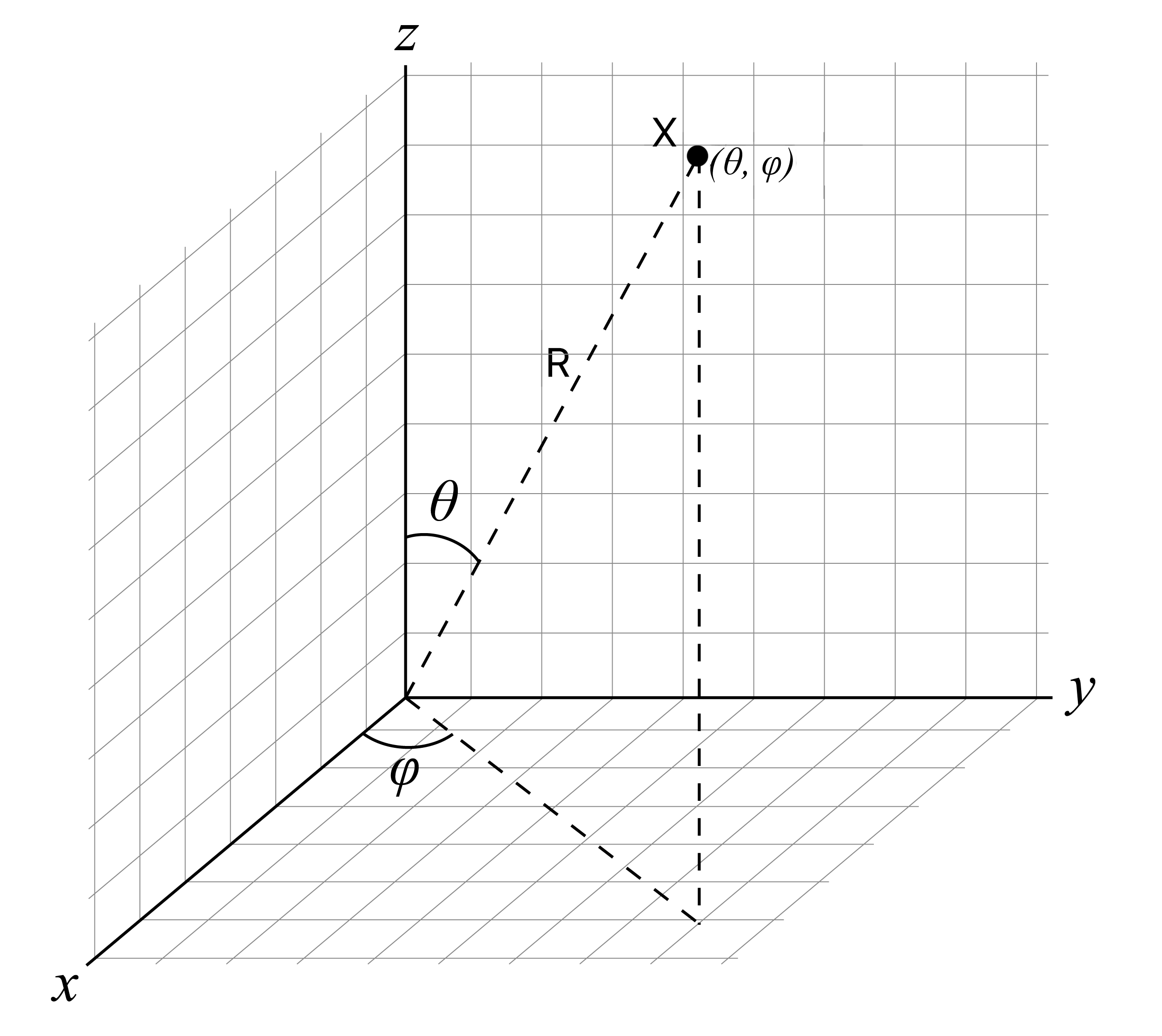
По прошествии задержки пользовательский интерфейс начинает своё движение. Рассмотрим произвольный кадр fj. Пусть P = (xUIfj, yUIfj, zUIfj) ∈ S – координаты центра пользовательского интерфейса, Q = (xsfj, ysfj, zsfj) ∈ S – координаты пересечения взгляда со сферой. Тогда мы можем сопоставить точкам P и Q пары чисел (θP, φP) и (θQ, φQ). 0° ≤ θX ≤ 180° для точки X вычисляется как угол между осью Oz и отрезком, соединяющим начало координат и точку X, 0° ≤ φX < 360° вычисляется как угол между осью Ox и проекцией отрезка, соединяющего начало координат с точкой X, на плоскость Oxy (см. рис. 2).
Таким образом получаем двумерное пространство Oθφ. Если соединить точки (θP,φP) и (θQ, φQ) в этом пространстве кратчайшей прямой линией, то мы получим отрезок, задающий изменение от положения P до положения Q. Вдоль этой линии пользовательский интерфейс движется с постоянной скоростью v градусов в кадр. Длина отрезка в пространстве Oθφ измеряется с помощью евклидовой нормы. Вам необходимо рассчитать, какое положение, заданное углами, будет у центра пользовательского интерфейса в следующем кадре и переместить его туда в конце текущего кадра.
Далее наступает момент времени следующего кадра fj + 1 и вышеописанная процедура повторяется для новых положений пользовательского интерфейса и пересечения взгляда со сферой. Как только в пространстве Oθφ расстояние до Q оказывается меньше, чем расстояние, проходимое интерфейсом за один кадр, пользовательский интерфейс фиксируется в пространстве и снова ожидает момент, при котором взгляд окажется за границей прямоугольника.
Помогите Руслану рассчитать, где будут находиться вершины прямоугольника пользовательского интерфейса в момент завершения расчёта последнего кадра.
Формат входного файла
В первой строке находятся 4 вещественных числа w,h,R,v и одно целое неотрицательное число k.
Следующая пара строк содержит по три вещественных числа в каждой: в первой даны числа (xp0, yp0, zp0) – начальное положение головы, во второй - (xd0, yd0, zd0) – начальное направление взгляда.
Затем для каждого f парами следуют строки: в первой даны числа (xpf, ypf, zpf) – текущее положение головы, во второй - (xdf, ydf,zdf) – текущее направление взгляда.
Формат выходного файла
Требуется вывести 4 строки, в каждой из которых содержится положение вершины прямоугольника пользовательского интерфейса. Первой выводится левая верхняя вершина, остальные – в порядке обхода по часовой стрелке (см. рис. 1).
Каждая координата округляется и выводится с точностью до 5-го знака после запятой.
Ограничения
0 < w,h ≤ 30;0 < R ≤ 20;
0 ≤ v ≤ 90;
0 ≤ k ≤ 200;
(xpf)2 + (ypf)2 + (zpf)2 < R2; (xdf)2 + (ydf)2 + (zdf)2 = 1, 0 ≤ f ≤ 4000.
Гарантируется, что центр пользовательского интерфейса и пересечения взгляда со сферой ни в какой момент времени не проходит через точки (0,0,R) и (0,0, − R).
Если существует два оптимальных пути движения, то выбирайте тот, который не проходит через скачок φ.
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|