Задача C. Баба Яга и волшебные часы ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Говорят, что у Бабы Яги есть волшебные механические часы без стрелок, висящие напротив печки. Поскольку время в Зачарованном лесу идет не так, как на остальной земле, циферблат часов разбит на n секторов, обозначенных числами от 1 до n, причём дважды: внутри циферблата и снаружи.
И если повернуть циферблат часов вокруг оси таким образом, чтобы сумма модулей разности соответствующих чисел стала равна s, то лишится Баба Яга всей своей магической силы. Да вот только как это сделать?
Формат входных данных
Две строки входных данных содержат натуральные числа n и s. Гарантируется, что для указанных входных данных ответ существует.
Обратите внимание, что значения переменных в этой задаче могут превышать возможные значения 32-битной целочисленной переменной, поэтому необходимо использовать 64-битные целочисленные типы данных (тип int64 в языке Pascal, тип long long в C++, тип long в Java и C#).
Формат выходных данных
Выведите число, которое нужно установить напротив единицы на внешнем кольце чисел. Если есть несколько подходящих ответов, выведите наименьший.
Ограничения
2 ≤ n ≤ 109
2 ≤ s ≤ 1018
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Решения, верно работающие при n ≤ 100, получат не менее 40 баллов.
Пояснение к примеру
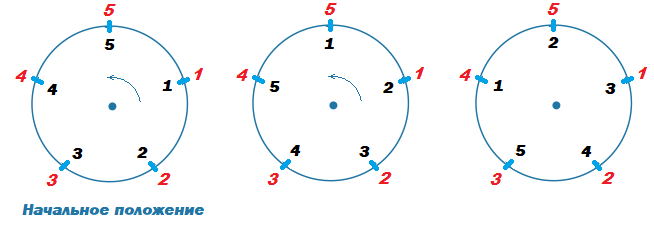
В примере дано n = 5 и s = 12. При начальном положении часов нужная сумма равна |1 − 1| + |2 − 2| + |3 − 3| + |4 − 4| + |5 − 5| = 0.
Повернём циферблат на одно деление. Сумма стала равна |1 − 2| + |2 − 3| + |3 − 4| + |4 − 5| + |5 − 1| = 8.
Повернём циферблат ещё на одно деление. Сумма стала равна |1 − 3| + |2 − 4| + |3 − 5| + |4 − 1| + |5 − 2| = 12. Нужная сумма набрана, напротив единицы на внешнем кольце установлена тройка на внутреннем кольце.
Примечание: нужной суммы можно добиться и при установке четвёрки, однако тройка меньше.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|