Задача 7I. Дерево отрезков ≡
| Автор: | Завгороднев А.А. | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход |
Условие
У Максима есть массив a размера n. Назовём подмассив от i до j правильным, если его размер (j − i + 1) равен степени двойки 2k для некоторого k. Максим выбирает какой-то правильный подмассив, на котором он строит дерево отрезков.
Дерево отрезков - это структура данных, которая представляет собой иерархическое дерево.
- Каждый узел дерева соответствует определенному отрезку.
- Листья дерева представляют собой базовые отрезки размера 1, то есть непосредственно элементы массива.
- Значение во внутреннем узле равно сумме значений дочерних узлов.
- Если внутренний узел соответствует отрезку от i до j, то левый дочерний узел будет соответствовать отрезку от i до i + j − 12, а правый от i + j + 12 до j.
- Значение в корне дерева равно сумме значений всех элементов массива, на котором строится дерево отрезков.
После этого Максим нумерует вершины дерева следующим образом: У корня будет номер 1, далее у его левого сына номер 2, а у правого номер 3. После этого он нумерует детей вершины номер 2, а потом вершины номер 3. И так далее он проводит эту операцию последовательно по возрастанию номеров вершин.
И уже после нумерации Максим находит его любимое число, характеризующее подмассив - сумму значений в узлах с нечетным номером. Это число Максим называет характеристикой подмассива.
Так как Максим очень любит эти числа, он просит вас найти сумму характеристик всех возможных правильных подмассивов массива a. Так как ответ может быть слишком большим, выведите его по модулю 109 + 7.
Формат входных данных
В первой строке находится одно целое число n - размер массива. (n ≤ 106).
Во второй строке располагается n чисел - значения массива a.
Формат выходных данных
Выведите одно целое число - сумму характеристик всех возможных правильных подмассивов массива a по модулю 109 + 7.
Пояснение к первому примеру:
Всего существует 8 правильных подмассивов:
- [1]: массив размера 1, дерево отрезков из одного элемента, номер которого 1, поэтому его характеристика равна 1.
- [2], [3], [4] - аналогично.
- [1, 2] - массив размер 2, дерево отрезков состоит из 3 узлов, корня и двух дочерних листьев. В корне находится значение 3. Корень имеет номер 1, а также элемент 2 имеет номер 3, поэтому характеристика этого подмассива равна 3 + 1 = 4.
- [2, 3], [3, 4] - аналогично.
- [1, 2, 3, 4] - массив размера 4, дерево отрезков из 7 узлов. Его структура показана на рисунке 1. Из рисунка видно что характеристика этого массива равна 10 + 7 + 2 + 4 = 23.
Итого сумма всех характеристик: (1 + 2 + 3 + 4) + ((3 + 2) + (5 + 3) + (7 + 4)) + (10 + 7 + 2 + 4) = 57.
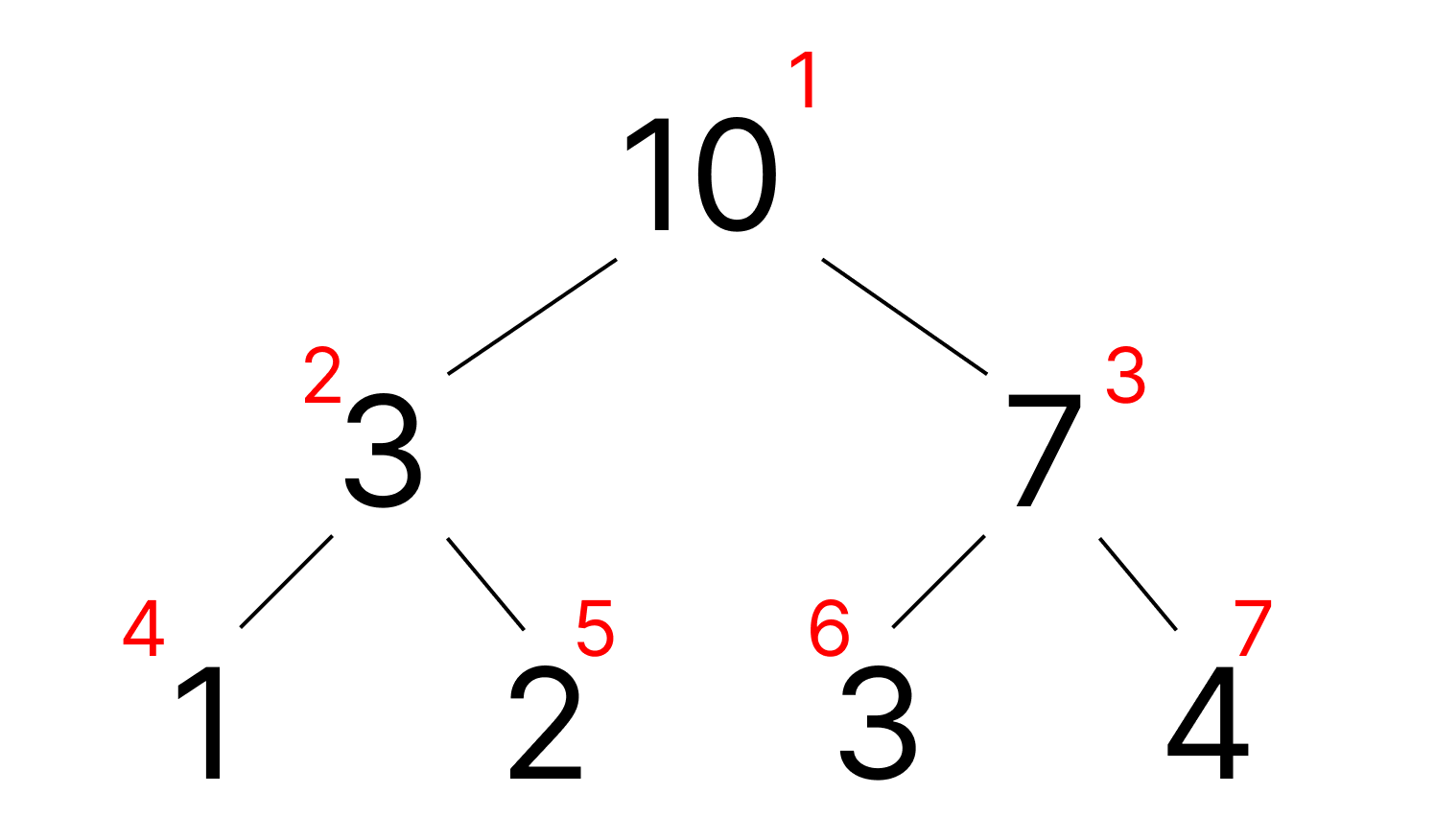
Дерево отрезков с номерами узлов.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
| 3 | |
|