Задача G4. Восстановление сетки ≡
| Автор: | И. Лудов, А. Кленин | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 256 Мб | |
| Выходной файл: | output.txt |
Условие
Турнир по олимпийской системе, состоящий из N раундов, проводятся между 2N участниками по следующей схеме: сначала составляется последовательность из расставленных в произвольном порядке игроков. В первом раунде первый в последовательности участник соревнуется со вторым, третий с четвёртым, и т.д. Проигравшие выбывают из турнира, и на втором раунде победитель первой пары играет с победителем второй, победитель третьей с победителем четвёртой, и т.д. Наконец, после N-го раунда остаётся ровно один участник, который становится победителем турнира.
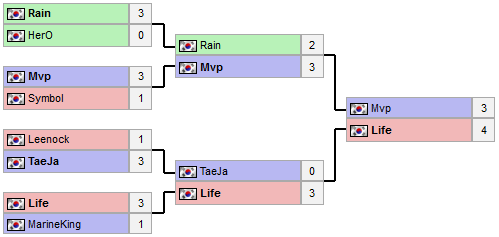 История таких турниров наглядно изображается с помощью специальной диаграммы, которая называется
турнирной сеткой.
История таких турниров наглядно изображается с помощью специальной диаграммы, которая называется
турнирной сеткой.
Назовём упорядоченной такую первоначальную последовательность участников, что в каждом матче сетки победителем оказывается первый участник. Например, первоначальная последовательность в приведённой справа сетке не соответствует этому условию — чтобы это исправить, нужно расположить участников в порядке: Life, MarineKing, TaeJa, Leenock, Mvp, Symbol, Rain, Hero.
Требуется по результатам всех проведённых в турнире матчей получить упорядоченную первоначальную расстановку участников.
Рекомендуется рассмотреть частичные решения
N ≤ 10;
Формат входного файла
Входной файла содержит целое число N, за которым следуют 2N − 1 пар чисел Wi Li, означающих, что участник с номером Wi победил участника с номером Li. Участники пронумерованы от 1 до 2N.
Формат выходного файла
Выходной файл должен содержать 2N целых чисел — номера участников, перечисленные в соответствии с упорядоченной первоначальной расстановкой.
Ограничения
1 ≤ N ≤ 20
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|