Задача A. Навигационные спутники Васи ≡
| Автор: | Dmitriy Merzlyakov | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 512 Мб | |
| Выходной файл: | output.txt | |||
| Максимальный балл: | 100 |
Условие
Юный программист Вася, вдохновившись принципом работы глобальных навигационных спутниковых систем, решил спроектировать собственную модель движения спутников вокруг Земли, которые в будущем могли бы определять его местоположение.
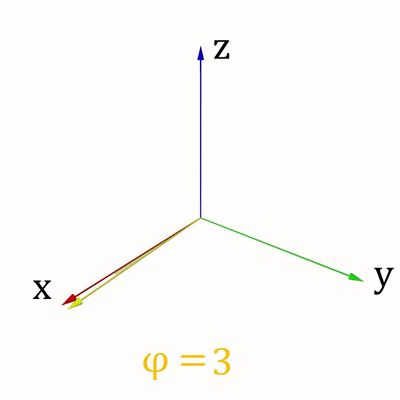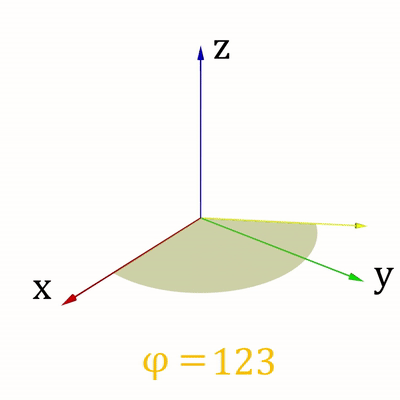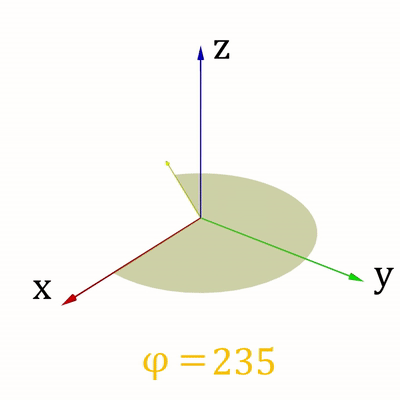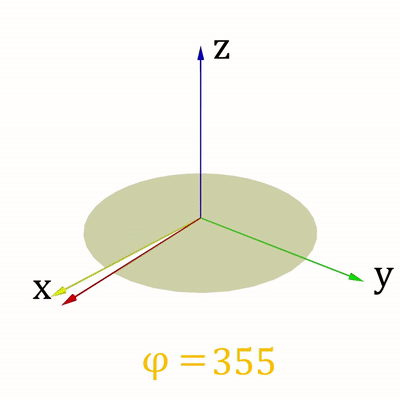
Для ведения своих расчётов Вася использует сферическую систему координат (r,φ, ψ), где r > = 0 – расстояние от точки до начала координат, φ ∈ [ − 90 ∘ ,90 ∘ ] - зенитный угол, ψ ∈ [0 ∘ ,360 ∘ ] - азимутальный угол. Направления изменения углов показаны на рис. 1 и рис. 2.
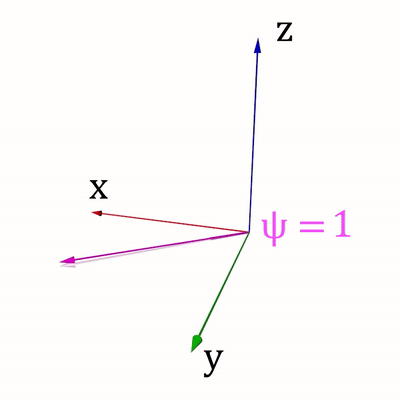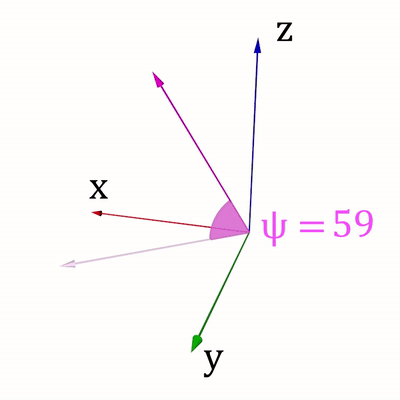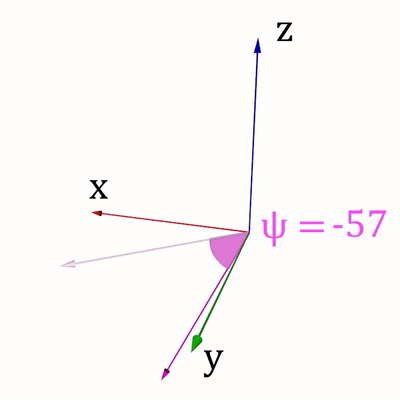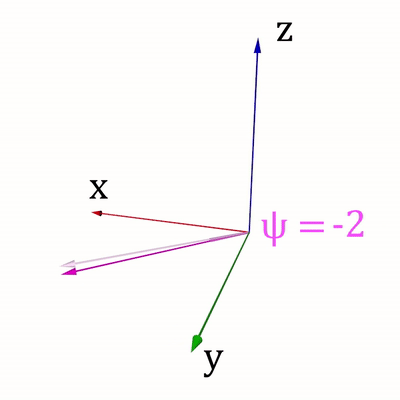 |
 |
В качестве модели Земли Вася взял идеальную сферу с уравнением r = 100 в сферических координатах. Поскольку первая координата зафиксирована, то каждая точка на поверхности будет описываться парой (φ,ψ).
Спутники Васи располагаются на k орбитах. Каждая i − ая орбита представляет из себя пространственную окружность радиуса Ri с центром в начале координат, лежащую в плоскости, заданной нормальным вектором n⃗ = (rn,φn,ψn). На каждой орбите находится mi точечных спутников, равноудалённых друг от друга. В начальный момент времени t0 = 0 первый спутник расположен в координатах (Ri,φi1,ψi1); все спутники вращаются против часовой стрелки, если посмотреть на плоскость орбиты со стороны нормали n⃗, и пронумерованы последовательно от первого спутника, начиная с 1. Каждый спутник на орбите совершает полный оборот за время ti.
Вася хочет написать программу, которая смогла бы оценить удачность выбранной системы спутников и расположения орбит. Для этого он выбирает целевую точку на поверхности сферы с координатами (φp,ψp) на сфере и пытается выяснить, сколько спутников в момент времени t будут находится на связи с целевой точкой. Будем говорить, что некоторый спутник находится на связи с целевой точкой, если отрезок, соединяющий спутник и целевую точку не пересекает сферу.
Помогите Васе написать такую программу.
Формат входного файла
В первой строке находится 2 числа φp и ψp – координаты целевой точки на поверхности сферы
Во второй строке находится число t – время для изучения положения спутников.
В третьей строке находится число k – количество орбит. Орбиты пронумерованы, начиная с 1, в порядке их появления.
Для каждой i − ой орбиты даны следующие данные:
- Число mi – количество спутников на i − ой орбите;
- Числа rn, φn, ψn - координаты вектора нормали плоскости вращения орбиты;
- Числа Ri, φi1, ψi1 – координаты первого спутника на орбите;
- Число ti – время полного оборота каждого спутника орбиты.
Формат выходного файла
Выходной файл содержит число kv – число спутников, находящихся на связи с целевой точкой в момент времени t.
Далее следуют kv строк, содержащих 2 числа – номера орбит и порядковых номеров спутников на этих орбитах, находящихся на связи с целевой точкой
в порядке возрастания обоих значений.
Если на связи нет ни одного спутника – выведите 0.
Ограничения
Гарантируется, что координаты первых спутников орбит лежат в их плоскостях вращения.
Гарантируется, что Ri > 100 для любого i ∈ {1,…,k}
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|