Задача C. Две диагонали ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
В правильном n-угольнике все вершины пронумеровали по часовой стрелке от 1 до n. После этого провели две не пересекающихся диагонали, соединив вершины 1 и a, а также b и c. Сколько существует диагоналей этого многоугольника, которые не пересекаются ни с одной из проведенных?
Формат входных данных
Единственная строка входного файла содержит четыре натуральных числа, записанных через пробел: n, a, b и c. Гарантируется, что все вершины различны. Гарантируется, что диагонали не совпадают со сторонами.
Формат выходных данных
Выведите одно неотрицательное целое число — ответ на задачу.
Ограничения
6 ≤ n ≤ 109
2 ≤ a, b, c ≤ n
b < c − 1
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Пояснение к примерам
В первом примере ни одной подходящей диагонали провести нельзя.
Во втором примере можно провести одну подходящую диагональ, соединив вершины 5 и 7.
В третьем примере можно провести три подходящих диагонали, соединив вершины 2 и 4, 6 и 12, а также 8 и 10.
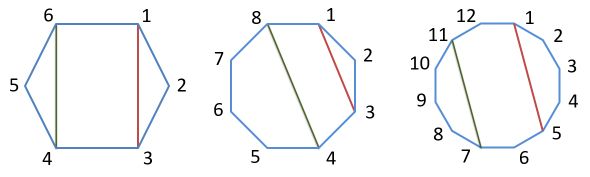
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|
| 3 | |
|