Problem G. Ground Works ≡
| Author: | ACM ICPC 2008-2009, NEERC, Northern Subregional Contest | Time limit: | 3 sec | |
| Input file: | ground.in | Memory limit: | 256 Mb | |
| Output file: | ground.out |
Statement
The Hilbert Mole is a small and very rare mole. The first and only specimen was found by David Hilbert at his backyard. This mole lives in a huge burrow under the ground, and the border of this burrow forms a Hilbert curve of n-th order (Hn).
Hilbert curves can be defined as follows. H1 is a unit square with open top side (fig. 1a), Hn consists of four copies of Hn − 1: bottom left and bottom right are copied without changes, top left is rotated 90∘ counter-clockwise and top right is rotated 90∘ clockwise. These small copies are connected by three segments of unit length (fig. 1b,c,d).
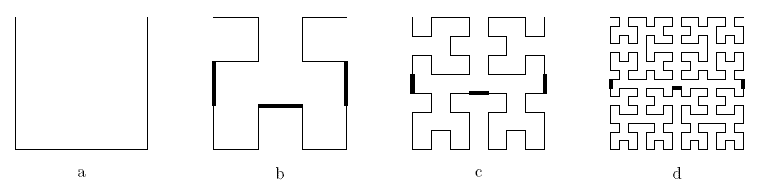
Trying to exterminate the mole, Mr. Hilbert fills the burrow with water (fig. 2). But air inside the burrow prevents water from filling it entirely. In this problem we suppose that air and water are incompressible and cannot leak throw the borders of the burrow. Your task is to find the total area of the burrow, filled with water.
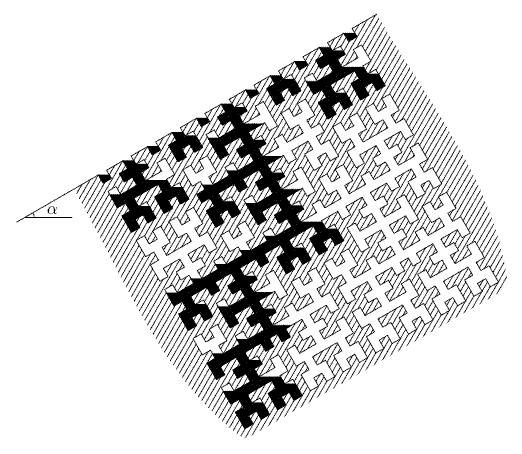
Note that water can flow over the obstacle only when its level is strictly higher. See examples on fig. 3 for further clarification.

Input file format
The first line of the input file contains two integer numbers: n and α — order of Hilbert curve and slope angle of surface in degrees.
Output file format
The first line of the output file must contain a single real number — the total area of the burrow, filled with water. The relative error of the answer must not exceed 10−7.
Constraints
1 ≤ n ≤ 12, 0 ≤ α < 90.
Sample tests
| No. | Input file (ground.in) |
Output file (ground.out) |
|---|---|---|
| 1 |
|
|
| 2 |
|
|
| 3 |
|
|
| 4 |
|
|