Problem E. Eye of the Admin ≡
| Author: | I. Ludov, A. Klenin | Time limit: | 2 sec | |
| Input file: | input.txt | Memory limit: | 64 Mb | |
| Output file: | output.txt |
Statement
Young system administrator Vasya is moving into a new server room. The room has a shape of convex polygon with LCD monitors mounted on some of the walls.
Monitors display the health data of various servers, so Vasya wishes to place his rotating chair such that he could observe them all without need to leave it.
 He moved all obstacles out of the way, so he can see any point
of any monitor from any place inside the room.
The only problem is that the image on LCD monitors deteriorates at
large viewing angles.
He moved all obstacles out of the way, so he can see any point
of any monitor from any place inside the room.
The only problem is that the image on LCD monitors deteriorates at
large viewing angles.
Viewing angle is an angle between the line connecting the eye of viewer with the point on monitor and the normal vector at that point. The angle can have values in range from 0 to π / 2. Vasya wants to place his chair at a point which minimizes a maximum viewing angle from him to any point of any monitor.
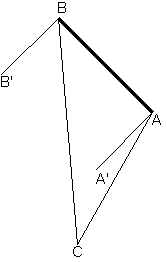
For example, in a picture line segment AB represents a monitor, point C — a chair, angles A′AC and B′BC are viewing angles, and the second of them is the maximum one.
Input file format
Input file contains the number of monitors N followed by N triplets of integers xi yi ai, where xi yi — coordinates of room vertexes in counter-clockwise order, ai = 1 if the wall between the i-th vertex and the next one is covered by a monitor, ai = 0 otherwise.
Output file format
Output file must contain floating point values x y — coordinates of point to place a chair. The point must lie inside the room.
If there is more than one solution, output any of them. The maximum viewing angle from point (x, y) must differ from the correct answer by at most 10 − 3 (measured in radians).
Constraints
3 ≤ N ≤ 40, 1 ≤ Σ ai ≤ 10, 0 ≤ xi, yi ≤ 105.Sample tests
| No. | Input file (input.txt) |
Output file (output.txt) |
|---|---|---|
| 1 |
|
|