Задача E. Enclosed by curves ≡
| Автор: | A. Baranov | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 512 Мб | |
| Выходной файл: | Стандартный выход |
Условие
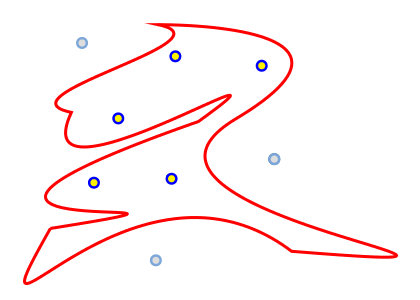
Начинающий программист Вася разрабатывает собственный векторный графический редактор. Помимо обычных примитивов (наподобие прямоугольников, окружностей, прямых) его редактор также поддерживает работу с объектами сложной формы, для описания которых используются сплайновые кривые.
Каждая такая кривая состоит из нескольких кусков, последовательно идущих друг за другом, каждый из которых задается параметрическим уравнением следующего вида:
Xi(t) = AXi ⋅ t3 + BXi ⋅ t2 + CXi ⋅ t + DXi;
Yi(t) = AYi ⋅ t3 + BYi ⋅ t2 + CYi ⋅ t + DYi,
где t — скалярный параметр, изменяющийся в диапазоне [0, 1].
Для описания сложных фигур Вася использует замкнутые сплайновые кривые. Одна из стоящих перед ним задач — определить для каждой из заданных точек попадание внутрь такой фигуры.
Формат входных данных
В начале входных данных содержится целое N, за которым следует 8 × N вещественных чисел, задающих коэффициенты соответствующих сплайнов
AXi, BXi, CXi, DXi,
AYi, BYi, CYi, DYi.
Далее записано целое число M, за которым следует 2 × M вещественных чисел, задающих координаты точек (Xj, Yj).
Формат выходных данных
Выходные данные должны содержать последовательность из M целых чисел
(ответов на каждый запрос):
1 — если соответствующая точка лежит внутри контура,
0 — если лежит снаружи.
Ограничения
В пределах заданной точности контур непрерывен и не имеет самопересечений.
Расстояние от каждой из точек до границы контура не меньше 10 − 5.
Контур целиком лежит внутри прямоугольной области [ − 10, 10] × [ − 10, 10].
1 ≤ N ≤ 1000, 1 ≤ M ≤ 105.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|