Задача L. LCA queries ≡
| Автор: | A. Usmanov | Ограничение времени: | 1 сек | |
| Ввод / вывод: | интерактивный | Ограничение памяти: | 256 Мб |
Условие
Данная задача является интерактивной и предполагает взаимодействие с сервером путем отправки и приема сообщений определенного вида.
Пусть у нас имеется полное двоичное дерево высоты N, состоящее из максимально возможного числа вершин.
Полагается, что все вершины такого дерева пронумерованы от 1 до 2N − 1.
Требуется определить номер корневой вершины, оперируя запросами на получение наименьшего общего предка (LCA) двух заданных вершин. Можно сделать не более N запросов.
Формат входных данных
В первой строке входных данных записано одно целое число N — высота дерева.
Протокол взаимодействия
Чтобы сделать запрос, ваша программа должна вывести "? X Y",
где X и Y — целые числа, номера вершин.
На каждый запрос программа жюри ответит целым числом —
номер вершины наименьшего общего предка.
Когда ваша программа определит корень дерева, она должна вывести "! X" и завершиться.
Если ваша программа сделает недопустимый запрос, то она получит вердикт "Presentation error". Если ваша программа превысит допустимое количество запросов, то она получит вердикт "Wrong answer".
Каждый запрос и вывод окончательного результата должен быть одиночной строкой
заканчивающейся одиночным переводом строки (\n).
Буфер вывода необходимо сбрасывать после каждой строки:
| Язык | C++ | Pascal | Java | Python |
| Код | cout.flush() |
flush(output) |
System.out.flush() |
stdout.flush() |
Ограничения
1 ≤ N ≤ 10
1 ≤ X, Y < 2N
Пояснение к примерам
В первом примере задано дерево:
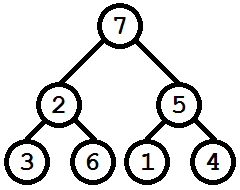
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|