Задача 60. Соседнее село ≡
| Автор: | Антон Карабанов | Ограничение времени: | 2 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Едем, едем в соседнее село на дискотеку,
Едем, едем на дискотеку со своей фонотекой,
Едем, едем с гаража угнав папину Победу,
Едем, едем в соседнее село на дискотеку.
...
Мурат Тхагалегов, "На дискотеку", 2014 г.
В Энском районе n сёл и деревень. По странному стечению обстоятельств, между двумя населёнными пунктами есть дорога только в том случае, если в их названиях не менее k одинаковых букв. Например, при k = 6 (и менее) между novoogаrevo и domodedovo есть дорога (в каждом названии по 4 буквы "o" и по одной букве "v" и "e"), а при k = 7 (и более) — дороги нет.
Два населённых пункта считаются соседними, если между ними есть дорога. Определите наиболее предпочтительный населённый пункт для организации дискотеки, чтобы на неё могли добраться из как можно большего количества соседних сёл и деревень.
Формат входных данных
Первая строка входного файла содержит два натуральных числа, записанных через пробел: n и k. В следующих n строках расположены названия населённых пунктов si, состоящие из не более чем 250 строчных английских букв. Гарантируется, что все названия попарно различны.
Формат выходных данных
Выведите название одного из населённых пунктов из входных данных — ответ на вопрос задачи. Если подходящих ответов несколько — выведите лексикографичеси наименьший. Гарантируется, что входные данные таковы, что в Энском районе есть хотя бы одна дорога.
Ограничения
2 ≤ n ≤ 500
1 ≤ k ≤ 100
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Пояснения к примерам
В первом примере при k = 1 дороги нет только между сёлами dedovo и myshkin (в из названиях нет ни одной общей буквы). Соответственно, эти два села будут соседними для четырёх населённых пунктов, а остальные четыре — для пяти. Из них лексикографически наименьшее babkino.
Во втором примере при k = 3 приведём граф дорог (смотри рисунок). При этом dedovo вообще не связан с остальными сёлами, у четырех сёл по три дороги, и только у koshkino их четыре.
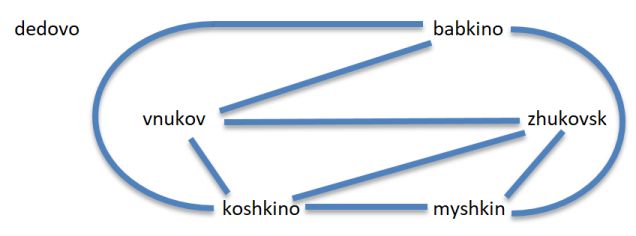
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|
| 2 | |
|