Задача 41. Колечко ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
...
Колечко, колечко, кольцо,
Давно это было, давно.
Зачем я колечко дарил,
Сердечко твоё бередил?
Александр Шаганов, "Колечко", 1996 г.
Одной из самых популярных дворовых игр детства автора этой задачи была "Колечко-колечко". Играли в неё так:
Игроки сидят в ряд и держат руки вместе, образуя форму чашки. Ведущий держит в руках небольшой предмет, например, монету, пуговицу или кольцо.
Ведущий по очереди обходит всех игроков, вкладывая им в «лодочку» свою, и произнося считалку: «Я ношу-ношу колечко и кому-то подарю». Водящий, вкладывая свои руки в руки участников, должен передать колечко любому из игроков так, чтобы остальные не догадались — кому именно.
Игрок, получивший «колечко», не должен подавать виду, что он его получил, а должен стараться сидеть с максимально невозмутимым лицом.

После того, как водящий прошёл всех игроков, он отходит от скамейки на несколько шагов и говорит: «Колечко, колечко, выйди на крылечко». Игрок, у которого в руках оказалось «колечко» должен вскочить со скамейки и подбежать к водящему.
Задача остальных игроков — не дать ему убежать и постараться удержать. Если у получившего колечко получилось выбежать, водящим становится он.
На крылечке n ребят играют в "Колечко". Начальная расстановка приведена на рисунке (игроки пронумерованы от 1 до n − 1, водящий — номер n). Спустя несколько минут расстановка была уже другой. Определите, какое наименьшее количество раз кольцо сменило владельца?
Формат входных данных
Первая строка входного файла содержит натуральное число n — количество ребят, принимающих участие в игре. В следующей строке через пробел расположена перестановка целых чисел от 1 до n — конечная рассадка игроков (водящий — последний).
Формат выходных данных
Выведите одно неотрицательное целое число — минимальное возможное количество переходов кольца от одного игрока к другому.
Ограничения
3 ≤ n ≤ 105
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Решения, верно работающие при n ≤ 1000, получат не менее 50 баллов.
Пояснение к примеру
В игре участвуют 5 человек. На рисунке изображен один из возможных способов достичь требуемого расположения игроков. Есть и другие, но все они требуют не менее пяти обменов.
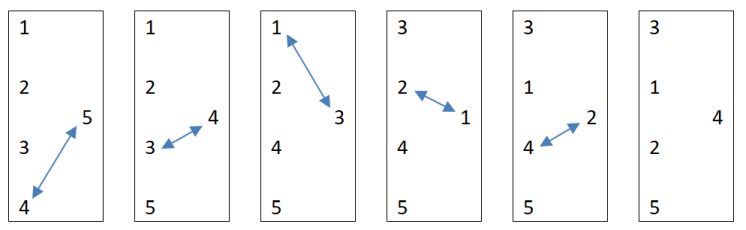
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|