Задача A. Компьютерный класс ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
В деревенскую школу наконец-то завезли компьютеры! Теперь можно убрать со столов счеты, логарифмические линейки и арифмометры и красиво расставить эти чудеса вычислительной техники.
В компьютерном классе парты стоят вдоль стен, образуя три непрерывных участка: два длинных и один короткий. Всего нужно расставить n компьютеров, соблюдая следующие ограничения:
1) количество компьютеров, расположенных на длинных участках, должно быть равным между собой, то есть если на одном участке a рабочих мест, то и на другом тоже a;
2) количество компьютеров, расположенных на коротком участке, должно быть строго меньше, чем на длинном, то есть если на коротком участке b рабочих мест, то b < a;
3) на каждом участке должен располагаться хотя бы один компьютер.
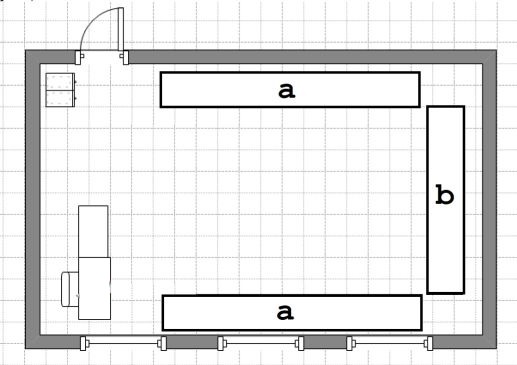
Помогите учителю информатики определить количество способов расставить все n компьютеров с учетом имеющихся ограничений.
Формат входных данных
Единственная строка входного файла содержит натуральное число n.
Формат выходных данных
Выведите одно неотрицательное целое число — ответ на вопрос задачи.
Ограничения
1 ≤ n ≤ 1018
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Решения, верно работающие при n ≤ 105, получат не менее 40 баллов.
Пояснение к примеру
В примере дано n = 20.
В первом случае компьютеры можно расставить так: a = 9 и b = 2.
Во втором: a = 8 и b = 4.
В третьем: a = 7 и b = 6.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 |
|
|