Задача 7B. В каждом рисунке - солнце ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход |
Условие
В столице Дальнего Востока проходит конкурс детских рисунков. Для оформления выставки работ финалистов организаторы планируют задействовать квадратный стенд. На одной стороне стенда будут размещены n вертикально ориентированных изображений одинакового размера w1×h1. На второй стороне стенда будут размещены m горизонтально ориентированных изображений одинакового размера w2×h2. При этом, согласно стандартам, расстояние между двумя рисунками, а также между рисунком и краем стенда должно быть не меньше 1, а стороны рисунков должны быть параллельны сторонам стенда.
Помогите организаторам рассчитать наименьшую сторону стенда, на котором возможно разместить все работы конкурсантов.
Формат входных данных
Единственная строка входного файла содержит шесть целых неотрицательных чисел, записанных через пробел: n, w1, h1, m, w2, h2. Гарантируется, что n и m не равны нулю одновременно.
Формат выходных данных
Выведите одно натуральное число - минимальный размер стенда.
Ограничения
0≤n,m≤109
1≤w1,h1,w2,h2≤109
w1≤h1
h2≤w2
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Решения, верно работающие при m=0, получат не менее 20 баллов.
Решения, верно работающие при w1=h2,h1=w2, получат не менее 20 баллов.
Пояснение к примеру
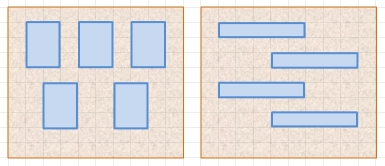
В примере нужно на одной стороне стенда разместить пять вертикально ориентированных рисунков размером 2×3 и четыре горизонтально ориентированных размером 5×1 на противоположной. Минимальный подходящий размер стенда 10, один из вариантов размещения изображений - на рисунке.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|