Задача D. Прыжки ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Одна из дворовых игр детства автора задачи называлась "Прыжки". Рисовался мелом прямоугольник, разбивался на квадраты с числами внутри от 1 до (по числу квадратов) и потом детвора пыталась по очереди пропрыгать по всем квадратам в порядке возрастания их номеров таким образом, чтобы ни разу не приземлиться на линии сетки.
Назовем расстоянием прыжка между квадратами с числами и расстояние между центрами этих квадратов (считая сторону квадрата равной 1). Так, расстояние прыжка между квадратами с числами 1 и 2 на приведенном на рисунке поле равно , между квадратами с числами 2 и 3 равно , между квадратами с числами 3 и 4 равно (вычисляется по теореме Пифагора).
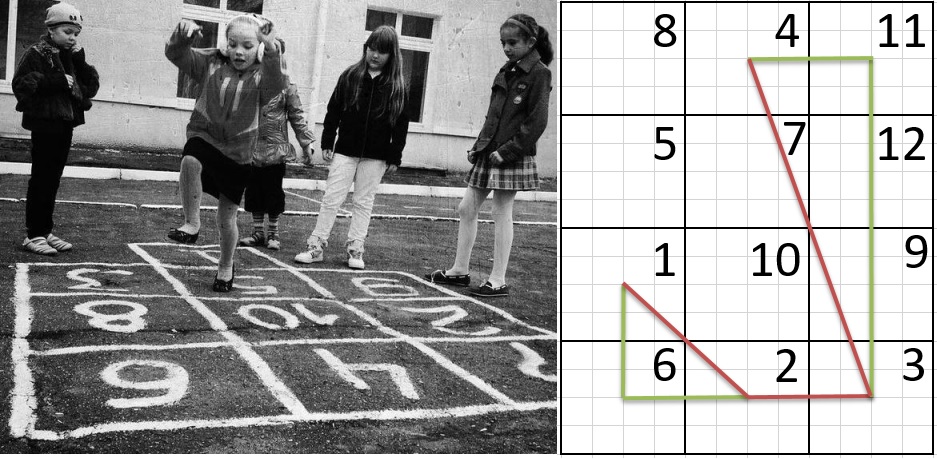
Тимофей еще маленький и прыгает не очень далеко, а квадраты с числами могут располагаться друг от друга на значительном расстоянии. По данному полю определите максимальное расстояние прыжка, требуемое для того, чтобы пройти испытание.
Формат входных данных
Первая строка входного файла содержит два натуральных числа, записанных через пробел: и . В следующих строках через пробел расположено по натуральных чисел — номера квадратов игрового поля. Гарантируется, что все составляют некоторую перестановку чисел от 1 до .
Формат выходных данных
Выведите одно натуральное число — максимального расстояния прыжка в данном поле.
Ограничения
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Пояснение к примеру
Наибольшее расстояние прыжка для данного в примере поля требуется для того, чтобы добраться с квадрата номер 3 до квадрата номер 4 (оно равно . Требуется вывести натуральное число — квадрат этого расстояния.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 |
|
|