Задача A. Four-dimensional polytope ≡
| Автор: | A. Baranov | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
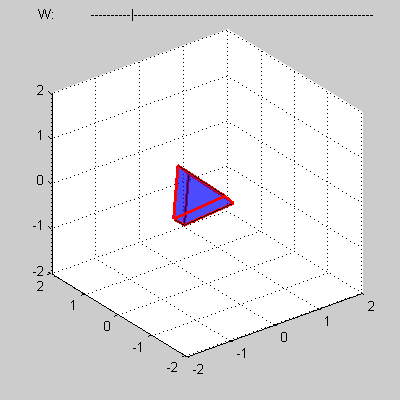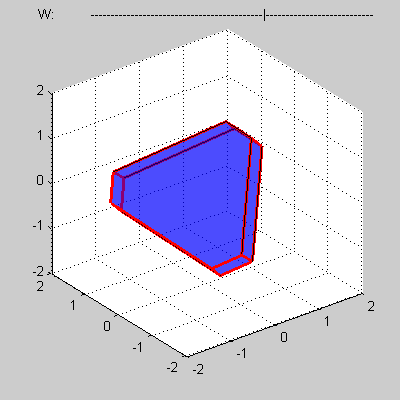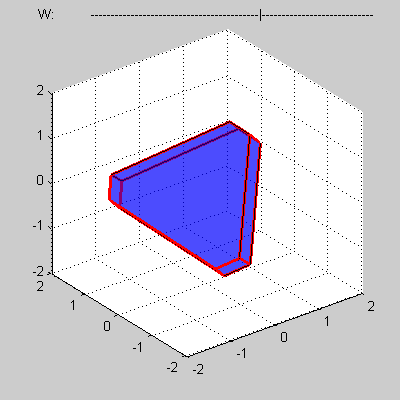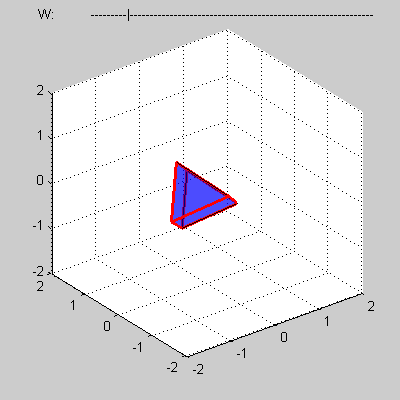
Пусть имеется некоторый выпуклый четырехмерный политоп, заданный в виде сетки, составленной из таких топологических элементов, как вершины, ребра, грани и трехмерные тела, для которых выполняются следующие условия.
Каждая вершина такого политопа задается четырьмя своими координатами (x, y, z, w). Каждое ребро представляет собой прямолинейный отрезок и задается парой соединяемых им вершин. Каждая грань представляет собой выпуклый многоугольник и задается набором своих ребер. Каждое тело представляет собой выпуклый многогранник и задается набором своих граней.
Сам политоп задается набором ограничивающих его трехмерных тел.
Требуется написать программу, вычисляющую объем сечения указанного политопа трехмерным подпространством при w = 0.
Формат входных данных
Во входных данных последовательно хранятся наборы сеточных элементов.
Вначале идет целое число V, за которым следует ровно 4 ⋅ V вещественных чисел, задающих координаты вершин.
Далее целое число E, за которым следует ровно 2 ⋅ E номеров вершин, попарно задающих ребра.
Далее идет целое число F, за которым следует ровно F граней, записанных в следующем виде.
Вначале целое число ребер N, за которым следует N номеров этих ребер.
Аналогичным образом записываются тела, заданные номерами своих граней.
Нумерация сеточных элементов каждого вида начинается с нуля.
Формат выходных данных
Выходные данные должны содержать объем с точностью не менее 5 знаков после запятой.
Ограничения
Гарантируется, что все сеточные элементы являются невырожденными.
Координаты вершин лежат в диапазоне от − 10 до 10.
Число элементов каждого вида не превосходит 1000.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|