Задача A. Equidistant shell ≡

Условие

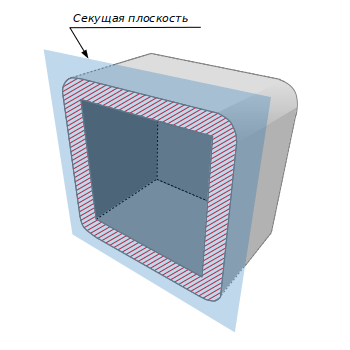
Эквидистантной оболочкой трехмерного тела называется множество внешних по отношению к нему точек, удаленных от него не более чем на заданное расстояние δ. На рисунке можно видеть пример эквидистантной оболочки для куба, представленной в разрезе.

Даны произвольный выпуклый многогранник и значение δ. Требуется написать программу, вычисляющую объем эквидистантной оболочки.

Формат входных данных

В начале входных данных хранится исходный многогранник, записанный в следующем виде.

Вначале идет целое число V, за которым следует ровно 3 ⋅ V вещественных чисел, задающих координаты вершин.

Далее целое число E, за которым следует ровно 2 ⋅ E номеров вершин, попарно задающих ребра.

Далее идет целое число F, за которым следует ровно F граней, записанных в следующем виде.

Вначале целое число ребер N, за которым следует N номеров ребер этой грани в произвольном порядке.

Нумерация всех указанных элементов начинается с нуля.

В конце входных данных записано вещественное значение δ.

Формат выходных данных

Выходные данные должны содержать объем с точностью не менее 5 знаков после запятой.

Ограничения

Все грани являются невырожденными и выпуклыми.

Координаты вершин лежат в диапазоне от  − 10 до 10.

Число элементов каждого вида не превосходит 100.

0 ≤ δ  ≤ 1

Примеры тестов

8
-1.00000 -1.00000 -1.00000
 1.00000 -1.00000 -1.00000
-1.00000  1.00000 -1.00000
 1.00000  1.00000 -1.00000
-1.00000 -1.00000  1.00000
 1.00000 -1.00000  1.00000
-1.00000  1.00000  1.00000
 1.00000  1.00000  1.00000

12
1 0
2 0
4 0
3 1
5 1
3 2
6 2
7 3
5 4
6 4
7 5
7 6

6
4 3 5 1 0
4 4 8 2 0
4 6 9 2 1
4 7 4 10 3
4 7 11 6 5
4 10 11 9 8

0.25

7.24355