Задача D. Квадраты в треугольнике ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Перед Тимофеем стоит серьёзная математическая задача — определить количество различных квадратов в прямоугольном ступенчатом "треугольнике" с катетом n.
Формат входных данных
В единственной строке записано одно натуральное число n.
Формат выходных данных
Выведете одно натуральное число — ответ на задачу. Гарантируется, что он не превысит 1018.
Ограничения
1 ≤ n ≤ 106
Система оценки и описание подзадач
Баллы за задачу начисляются только в случае, если все тесты успешно пройдены.
Подзадача 1: 1 ≤ n ≤ 1000, баллы: 30.
Подзадача 2: нет дополнительных ограничений, баллы: 70.
Пояснения к примерам
Комментарий к первому примеру:
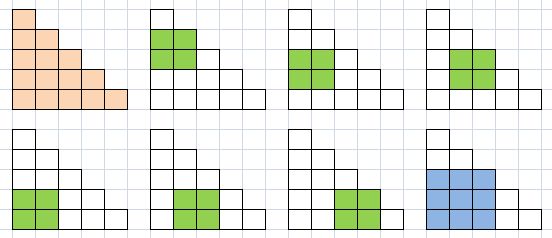
"Треугольник" с катетом пять вмещает 15 квадратов со стороной один, 6 квадратов со стороной два и 1 квадрат со стороной три. Всего 22 различных квадрата.
Комментарий ко второму примеру:
"Треугольник" с катетом восемь вмещает 36 квадратов со стороной один, 21 квадрат со стороной два, 10 квадратов со стороной три и 3 квадрата со стороной четыре. Всего 70 различных квадратов.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 |
|
|
| 2 |
|
|