Problem F. Four-dimensional polytope ≡
| Author: | A. Baranov | Time limit: | 1 sec | |
| Input file: | Standard input | Memory limit: | 256 Mb | |
| Output file: | Standard output |
Statement
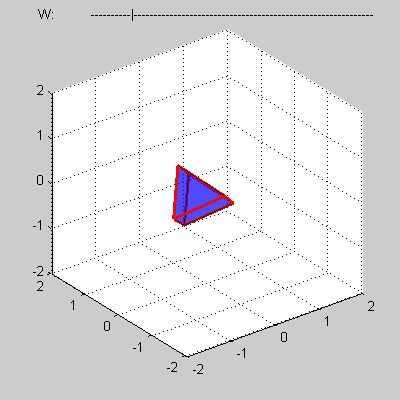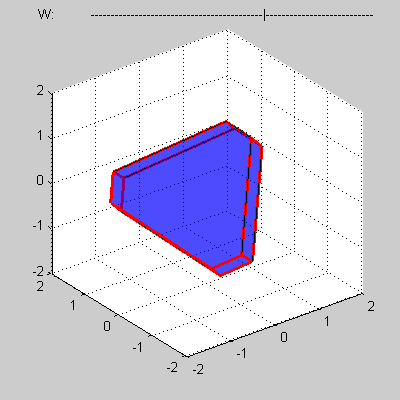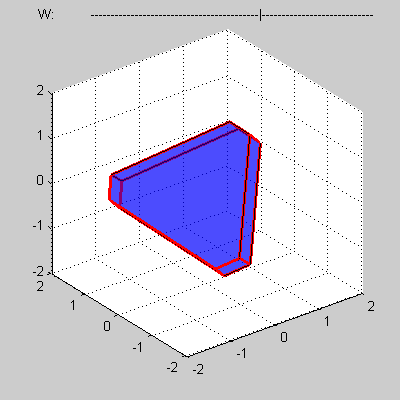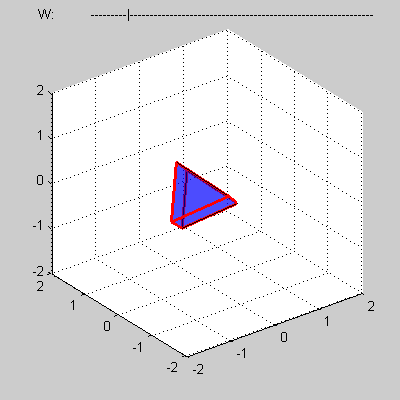
Consider some convex four-dimensional polytope that presented by a mesh composed of such elements as vertices, edges, faces and three-dimensional bodies.
Each vertex is represented by four coordinates (x, y, z, w). Each edge is a straight line segment and is represented by a pair of vertices connected by it. Each face is a convex polygon and is represented by a set of its edges. Each body is a convex polyhedron and is represented by a set of its faces.
The polytope itself is specified by set of three-dimensional bodies bounding it.
You program must calculate volume of a cross-section of the polytope by 3D sub-space with w = 0.
Input format
Input data contains sequence of the mesh elements.
First there is the integer V, followed by exactly 4 ⋅ V real numbers that are coordinates of the vertices.
Next, integer E, followed by exactly 2 ⋅ E numbers of the vertices, defining the edges pairwise.
Next is the integer F, followed by exactly F faces represented in the following format.
First integer number of edges N, followed by N indices of edges of this face.
The bodies specified by set of their faces are written in the same way.
Indices of the all elements start from zero.
Output format
Output data must contain the volume with an accuracy of at least 5 digits after decimal point.
Constraints
It is guaranteed that all mesh elements are non-degenerate.
Vertex coordinates are in the range from − 10 to 10.
Count of elements of each kind does not exceed 1000.
Sample tests
| No. | Standard input | Standard output |
|---|---|---|
| 1 | |
|