Дробь в LATeX-е ≡

Автор:?   Ограничение времени:2 сек
Входной файл:frac.in   Ограничение памяти:200 Мб
Выходной файл:frac.out  

Условие

Издательская система LATeX предназначена для верстки сложных научно-технических текстов с большим количеством формул. Исходный файл для системы LATEX пишется на языке TEX и представляет собой текст документа, в который включены специальные символы и команды. Специальные символы и команды описывают размещение текста, в частности в математических формулах. Команда представляет собой последовательность латинских букв (регистр важен), перед которой стоит символ "\". Так, команда \frac предназначена для описания дроби, в которой числитель расположен над знаменателем. Рассмотрим простейшую структуру команды \frac.

Комадна \frac имеет два параметра - числитель и знаменатель. Перед самой командой не обязательно ставить пробел. Следом за ключевым словом \frac записываются числитель и знаменатель. Если числитель и знаменатель имеют длину более одного символа, они заключаются в фигурные скобки. Если числитель или знаменатель записываются одной буквой или цифрой, их можно не брать в фигурные скобки. Если числитель записывается одним символом, то он отделяется от \frac хотя бы одним пробелом. Если знаменатель записывается одним символом, то он не отделяется пробелом от числителя. Произвольное ненулевое количество пробелов считается синтаксически эквивалентным одному пробелу. Нельзя разделять пробелами на части ключевое слово \frac.

Дадим также формальное определение выражения для нашей задачи:

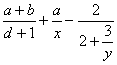Здесь вертикальная черта | означает "или", заключенная в квадратные скобки часть может отсутствовать, а символы, записаные в кавычках обозначают самих себя. Печатный символ - любой символ с ASCII кодом от 32 (пробел) до 127. Например, выражение записывается на языке TEX как
\frac{a+b}{d+1}+\frac ax -\frac 2 {2+\frac{3}{y}}

Чтобы в печатаемом документе вывести формулу, необходимо вычислить ее высоту для используемого при печати шрифта. Шрифт определяет размеры S - высоту отдельного символа и D - высоту горизонтальной дробной черты. Значения S и D задаются целыми числами. Ваша задача - для заданного выражения на языке TEX вычислить высоту формулы.

Отметим, что если две дроби принадлежат одному выражению, то их дробные черты записываются на одном уровне, а если нет (например, относятся к числителям или знаменателям различных дробей), это свойство может и не выполняться. Чтобы проиллюстрировать применение этого правила, приведем два примера: 

\frac{a+b}{\frac cd}+\frac{\frac ef}{g+h}
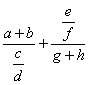\frac{a+b+c}{\frac{\frac de}{g+h}}+\frac{i+j+k}{\frac{l+m}{\frac no}}

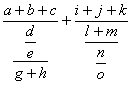Формат входного файла

В первой строке находятся целые положительные числа S и D. Следующая строка содержит описание формулы на TEX-е, длина строки не более 200 символов. Гарантируется, что формула синтаксически корректна, то есть фигурные скобки образуют правильную скобочную последовательность и строка содержит только печатные символы. Все символы "\", встречающиеся в строке относятся к некоторой командной последовательности (не обязательно \frac), можете считать, что все прочие командные последовательности задают символы, высота которых равна S. Числитель и знаменатель каждой дроби содержат хотя бы по одному символу, вся формула содержит хотя бы один символ.

Формат выходного файла

Выведите в выходной файл единственное число — высоту формулы.

Ограничения

1 ≤ S, D ≤ 10000

Примеры тестов

№ Входной файл (frac.in) Выходной файл (frac.out)
1 
10 2
\frac{a+b}{d+1}+\frac ax -\frac 2 {2+\frac{3}{y}}
 
34
2 
10 2
no fractions here
 
10
3 
10 2
\frac        {\alpha}          {\beta+\sin{2+x}}
 
22
4 
10 2
\cos{\frac{\alpha}b}
 
22
5 
10 2
\frac a  {sin{a}}
 
22
6 
10 2
\frac{a+b}{\frac cd}+\frac{\frac ef}{g+h}
 
46
7 
10 2
\frac{a+b+c}{\frac{\frac de}{g+h}}+\frac{i+j+k}{\frac{l+m}{\frac no}}
 
46
0.281s 0.021s 21