Задача B. Антон и CATS ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Антон - автор задач по спортивному программированию. Он живет на Дальнем Востоке и для организации олимпиад по информатике использует тестирующую систему ДВФУ. Сформировав пакет с очередной задачей, Антон загружает её на сервер в свою папку и управляет ею через страницу web-интерфейса.

Иногда Антону становится интересно, сколько всего задач он уже придумал? К сожалению, удобной нумерации задач на странице нет (каждой задаче можно назначить букву английского алфавита, но при большом количестве задач это не помогает). Поэтому Антон пользуется таким приемом: он выбирает из раскрывающегося списка число k - количество задач, которое будет отображаться на одной странице. После этого он переходит по ссылке на последнюю страницу с задачами (пусть ее номер будет x) и считает количество задач на этой странице y. Осталось посчитать общее количество задач по формуле k ⋅ (x − 1) + y.
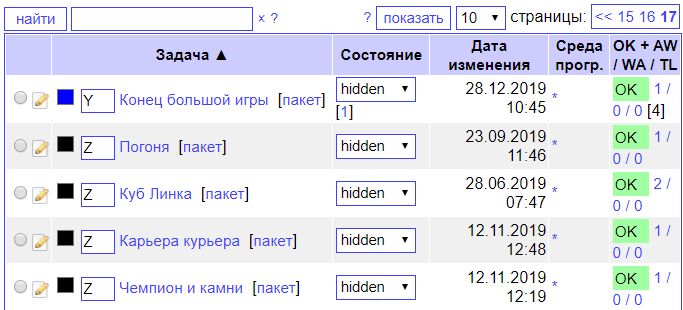
На рисунке выше Антон выбрал представление по 10 задач на одной странице, перешел на последнюю из 17 страниц и увидел на ней 5 задач. По формуле 10 ⋅ 16 + 5 он определил, что всего загружено 165 задач. Поскольку умножает Антон мгновенно, а считает задачи медленно, помогите ему выбрать такое k, чтобы количество задач на последней странице y было как можно меньше.
Формат входных данных
Первая строка входного файла содержит два натуральных числа, записанных через пробел: n - общее количество придуманных Антоном задач (сам Антон его не знает) и m - количество способов выбрать число k. В следующей строке через пробел в порядке возрастания расположены m натуральных чисел ki.
Формат выходных данных
Выведите одно натуральное число, содержащееся во второй строке входных данных, при выборе которого Антон увидит наименьшее число своих задач на последней странице. Если подходящих чисел несколько - выведите наибольшее.
Ограничения
1 ≤ n ≤ 109
1 ≤ m ≤ 105
1 ≤ ki ≤ 109
n ≤ km
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Пояснение к примеру
Минимальное возможное количество задач на последней странице равно пяти. Это число можно получить, выбрав представление по 10, 20 или 40 задач на одной странице. Наибольшее из этих чисел: 40.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 |
|
|