Задача D. Лототрон ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Из окна своей квартиры Тимофей наблюдает, как несколько молодых людей спортивного телосложения устроили на тротуаре розыгрыш денежных призов. Они собирают с желающих поиграть прохожих взнос за игру, а потом запускают лототрон.
Лототрон представляет собой заполненный n шарами лотерейный барабан треугольной формы. Каждый шар имеет уникальный номер от 1 до n. Шары вынимают снизу по одному, и на освободившееся место опускается один из двух шаров, находящихся выше, на освободившееся место опускается один из двух шаров, находящихся еще выше, и так далее. Если над освободившимся местом находится всего один шар - опускается он. Когда над освободившимся местом больше нет шаров, организаторы приступают к извлечению снизу нового шара.
Перед игрой лототрон заполняют шарами и несколько раз раскручивают, поэтому начальная расстановка шаров в барабане случайна. В игре побеждает игрок, верно указавший, какой шар будет извлечен k-м по счету. Спустя несколько раундов Тимофей заметил интересную особенность: на свободное место из двух шаров сверху всегда опускается шар с большим номером, а это значит, что последовательность извлечения шаров однозначно определяется их исходной расстановкой в лототроне. Поскольку в игре постоянно побеждают одни и те же "случайные" прохожие, Тимофей понял, что они пользуются заранее составленной компьютерной программой в своем смартфоне, позволяющей им быстро определять последовательность извлечения шаров. А Вы сможете составить такую программу?
Формат входных данных
В первой строке входного файла через пробел записаны два целых числа n и k - количество шаров в барабане и количество шаров, которые будут извлечены.
Во второй строке через пробел записаны n последовательных натуральных чисел от 1 до n - начальная расстановка шаров в барабане. Первый по счету шар лежит в нижнем (первом) ряду барабана, над ним (во втором ряду слева направо) - второй и третий, над ними в том же порядке шары с четвертого по шестой и так далее. Последний ряд может быть неполным, в этом случае шары в этом ряду лежат подряд вплотную к левому краю барабана.
Формат выходных данных
В единственной строке выходного файла запишите одно натуральное число - номер шара, который будет извлечен k-м по счету.
Ограничения
1≤k≤n≤1000.Система оценки и описание подзадач
Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи успешно пройдены.
Подзадача 1: k=2, баллы: 10.
Подзадача 2: k=3, баллы: 20.
Подзадача 3: нет ограничений, баллы: 70.
Пояснения к примеру 1
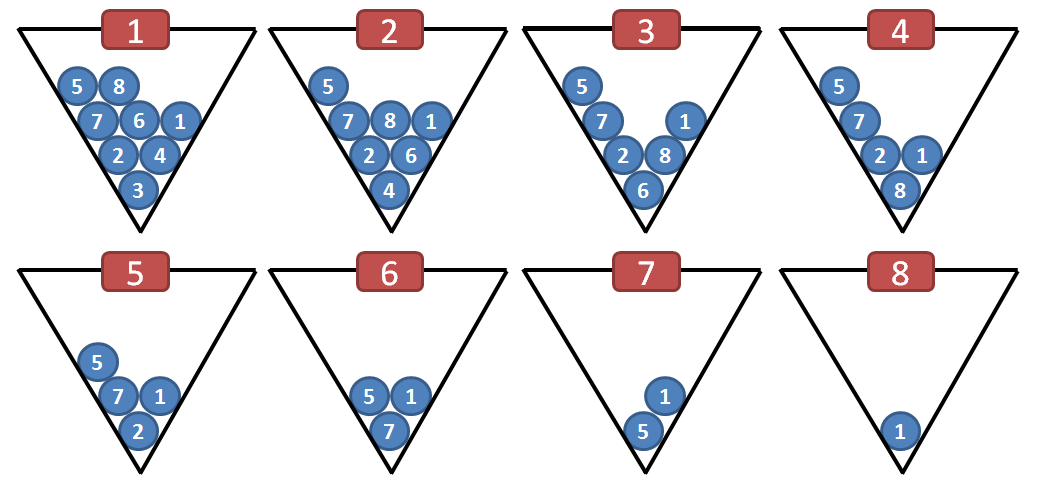
На первом шаге снизу извлекается шар номер 3. На освободившееся место "претендуют" два шара: 2 и 4. Вниз переходит шар номер 4 - его номер больше. На место этого шара "претендуют" два шара: 6 и 1. Вниз переходит шар номер 6 - его номер больше. Над свободным местом находится единственный шар номер 8 - он переходит вниз.
На втором шаге снизу извлекается шар номер 4. На освободившееся место "претендуют" два шара: 2 и 6. Вниз переходит шар номер 6. На место этого шара "претендуют" два шара: 4 и 1. Вниз переходит шар номер 4. Над свободным местом больше шаров нет.
Таким же образом будут последовательно извлечены шары с номерами 6, 8, 2, 7 и 5. Восьмым по счету будет шар номер 1.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 | |
|