Задача F. Звездчатый многоугольник ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Несколько лет назад Тимофей (после долгих мучений) научился рисовать пятиугольную звезду. Сначала он расставлял пять точек на окружности на равном расстоянии друг от друга. После этого он соединял эти точки отрезками по часовой стрелке от первой вершины, пропуская ровно одну вершину. А сегодня на занятии кружка по математике Тимофей узнал про звездчатые многоугольники. Строятся они так: каждая вершина правильного n-многоугольника соединяется с m-ной от неё на окружности по часовой стрелке. Звезда, полученная таким образом, обозначается как {n/m} (например, пятиконечная звезда, которую рисовал Тимофей в детстве, обозначается как {5/2}). При этом точки пересечения сторон между собой не рассматриваются как вершины. Такая звезда имеет n вершин и n сторон, также как и правильный n-угольник.
Дома Тимофей выбрал число n и начал рисовать все возможные звездчатые n-угольники от {n/1} до {n/n-1}. Некоторые рисунки ему понравились больше других - в них проведенные стороны пересекались между собой и не распадались на несколько связанных групп (как например, в фигуре {6/2} проведенные стороны распадаются и образуют два треугольника). Такие звезды Тимофей называет красивыми. Теперь Тимофею хочется по заданному n узнать количество различных красивых звездчатых n-угольников.
Формат входных данных
Единственная строка входного файла содержит одно натуральное число n - количество вершин.
Формат выходных данных
Выведите одно неотрицательное целое число - количество различных красивых звездчатых многоугольников.
Ограничения
3≤n≤105
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Пояснение к примеру
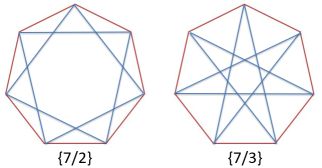
В примере даны вершины правильного семиугольника. Стороны звездчатого многоугольника {7/1} не пересекаются, {7/2} и {7/3} - красивые, {7/4} совпадает с {7/3}, а {7/5} совпадает с {7/2}. Стороны звездчатого многоугольника {7/6} не пересекаются. Всего красивыми являются два варианта.
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 |
|
|