Задача A. Треугольник в параллелепипеде (ОНТИ) ≡

Условие

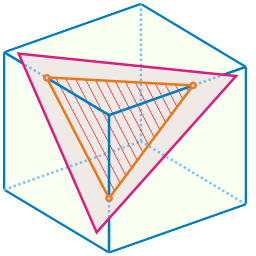
Имеется параллелепипед со сторонами, параллельными осям координат: D = { (x, y, z): x_min ≤ x ≤ x_max, y_min ≤ y ≤ y_max, z_min ≤ z ≤ z_max} и некоторый треугольник T, заданный координатами своих вершин: (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃).

Требуется определить площадь части треугольника T, которая лежит внутри параллелепипеда D.

Формат входных данных

В начале входных данных записаны координаты двух наиболее удаленных вершин параллелепипеда: (x_min, y_min, z_min), (x_max, y_max, z_max).

Далее следуют координаты вершин треугольника: (x₁, y₁, z₁), (x₂, y₂, z₂), (x₃, y₃, z₃).

Формат выходных данных

Выходные данные должны содержать площадь, указанную с точностью до 5-го знака после запятой.

Ограничения

Вершины треугольника не лежат на одной прямой.

x_min ≤ x_max, y_min ≤ y_max, z_min ≤ z_max.

Примеры тестов

-1.00000 -1.00000 -1.00000
 1.00000  1.00000  1.00000

-1.25000  0.56000  1.28090
-1.30000 -1.29010 -0.75000
 0.60790 -1.30700  1.30600

0.97386

-1.50000 -1.50000  1.00000
 0.50000  0.00000  1.50000

-3.70980  0.67000  3.20000
-4.60000 -1.86010  3.80250
 1.00000 -1.25000  4.10900

0.00000