Задача C. Мост ≡
| Входной файл: | input.txt | Ограничение времени: | 2 сек | |
| Выходной файл: | output.txt | Ограничение памяти: | 256 Мб | |
| Максимальный балл: | 100 |
Условие
Город Соколовка находится на берегах реки Флатовка, протекающей с юга на север. Жители города очень деловые и поэтому написали письмо мэру города с просьбой построить новый мост через реку для того, чтобы можно было перемещаться из одной части города в другую без автомобильных пробок. Однако возможности городского бюджета ограничены, поэтому мэр решил построить мост минимально возможной длины. Вдоль реки по обоим берегам проходят автомобильные дороги, поэтому выезд на мост можно сделать в любом месте.
Для упрощения задачи поиска местоположения моста, можно представить, что берега реки представляют собой ломаные, бесконечные в обе стороны. Введем координатную систему таким образом, чтобы ось OY была направлена с юга на север, а ось OX – с запада на восток. Левый берег начинается лучом, направленным на юг из точки (x1, 1, y1, 1), продолжается отрезками
(x1, 1, y1, 1) − (x1, 2, y1, 2), (x1, 2, y1, 2) − (x1, 3, y1, 3), …, (x1, m−1, y1, m−1) − (x1, m, y1, m)
и заканчивается лучом, направленным на север из точки (x1,m, y1, m). Аналогично, правый берег реки начинается лучом, направленным на юг из точки (x2, 1, y2, 1), продолжается отрезками(x2, 1, y2, 1) − (x2, 2, y2, 2), (x2, 2, y2, 2) − (x2, 3, y2, 3), …, (x2, n−1, y2, n−1) − (x2, n, y2, n)
и заканчивается лучом, направленным на север из точки (x2, n, y2, n).Помогите мэру города выяснить, мост какой минимальной длины можно построить.
Формат входного файла
Первая строка входного файла содержит целое число m. Следующие m строк содержат по два целых числа – координаты вершин ломаной левого берега: x1,1; y1,1, x1,2; y1,2, …, x1,m; y1,m.
Следующая строка входного файла содержит целое число n. Следующие n строк содержат по два целых числа – координаты вершин ломаной правого берега: x2,1; y2,1, x2,2; y2,2, …, x2,n; y2,n.
Известно, что x1,1 < x2,1, каждая из ломаных не имеет самопересечений и самокасаний, ломаные не имеют общих точек. Все отрезки каждой из ломаных имеют положительную длину. Все координаты не превосходят 104 по абсолютной величине.
Формат выходного файла
Выведите в выходной файл одно вещественное число: минимальную возможную длину моста. Ваш ответ будет проверяться с точностью 10−5.
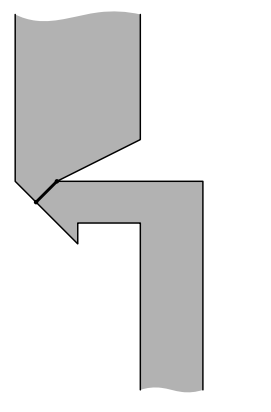
Оптимальное положение моста показано на следующем рисунке:
Ограничения
2 ≤ m, n ≤ 100
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 |
|
|