Задача M. C3-2009 ≡
| Автор: | Демо ЕГЭ 2009, Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 64 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Два игрока играют в следующую игру. На координатной плоскости стоит фишка. Игроки ходят по очереди. В начале игры фишка находится в точке с координатами (x, y). Ход состоит в том, что игрок перемещает фишку из точки с текущими координатами в одну из n точек: или в точку с координатами (x+a1, y+b1), или в точку с координатами (x+a2, y+b2), ..., или в точку с координатами (x+an, y+bn). Выигрывает игрок, после хода которого расстояние по прямой от фишки до точки с координатами (0, 0) не меньше z единиц. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход?
Формат входных данных
Первая строка входного файла содержит четыре натуральных числа, записанных через пробел x, y, z и n - начальные координаты фишки, условие победы и число возможных ходов. В следующих n строках через пробел указаны ai и bi - направления перемещения фишки для каждого хода.
Формат выходных данных
Выведите 'First' или 'Second' (без кавычек), в зависимости от того, победит первый или второй игрок.
Ограничения
2≤n≤5
0≤x,y,z≤300
x2+y2<z2
0≤a1,bi≤100
0<a1+bi
Система оценки и описание подзадач
Баллы за каждый тест начисляются независимо.
Пояснение к примеру:
Пример подробно рассмотрен в разборе Демонстрационного варианта ЕГЭ по информатике 2009. Ниже в таблице указаны выигрышные ходы второго игрока.
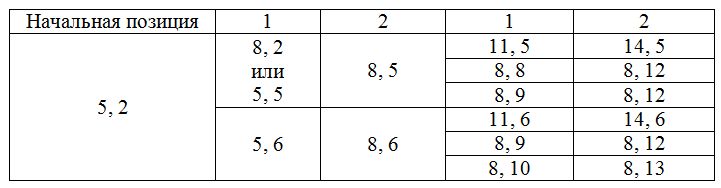
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 |
|
|