Задача C. Игральные кости ≡
| Автор: | Антон Карабанов | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 256 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
Игральная кость — это кубик, на каждой из шести граней которого нанесены числа от 1 до 6. Традиционно противоположные стороны кубика в сумме дают семь, причём грани 1, 2 и 3 имеют общую вершину (соответственно, общую вершину также имеют грани 4, 5 и 6).
У Тимофея, страстного поклонника настольных игр, накопилось очень много кубиков одного размера. Сегодня он обнаружил, что может сложить их в прямоугольный параллелепипед с длинами сторон a, b и c кубиков. Но Тимофей хочет найти такое расположение кубиков, чтобы сумма чисел на сторонах параллелепипеда была наибольшей.
Формат входных данных
В единственной строке входного файла через пробел записаны три натуральных числа a, b и c - размеры параллелепипеда.
Формат выходных данных
В единственной строке выходного файла запишите одно целое число - максимально возможная сумма чисел на внешней поверхности параллелепипеда. Гарантируется, что ответ не превысит 1018.
Ограничения
1≤a≤b≤c≤108.Система оценки и описание подзадач
Баллы за каждую подзадачу начисляются только в случае, если все тесты этой подзадачи успешно пройдены.
Подзадача 1: a=1, b=1, баллы: 20.
Подзадача 2: a=1, баллы: 20.
Подзадача 3: нет дополнительных ограничений, баллы: 60.
Пояснения к примерам
В первом примере у Тимофея два кубика. Логично установить их так, чтобы они соприкасались гранями, на которых нанесено число 1. Тогда снаружи можно увидеть сумму чисел, равную 2⋅(6+5+4+3+2)=40.
Во втором примере у Тимофея 27 кубиков из которых он строит куб размером 3:3:3. Максимальная сумма чисел, которые будут видны снаружи, равна 288. Один из примеров такого расположения и развертка куба внизу на рисунке.
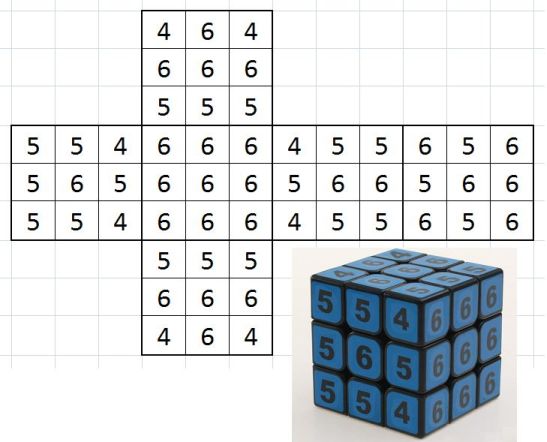
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 |
|
|
| 2 |
|
|