Задача E. Березовая аллея ≡
| Автор: | Центральная предметно-методическая комиссия по информатике | Ограничение времени: | 2 сек | |
| Входной файл: | birch.in | Ограничение памяти: | 512 Мб | |
| Выходной файл: | birch.out | |||
| Максимальный балл: | 100 |
Условие
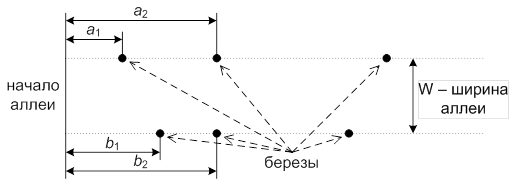
На краю деревни растет старая березовая аллея. Аллея имеет форму прямой полосы шириной W метров. Вдоль левой стороны аллеи растет N берез, а вдоль правой — M берез, при этом i-я береза с левой стороны аллеи находится на расстоянии ai метров от начала аллеи, а j-я береза с правой стороны — на расстоянии bj метров от начала аллеи.
Отдыхая в деревне прошедшим летом, один юный информатик обнаружил, что кору берез стали грызть зайцы.
Чтобы защитить деревья от зайцев, мальчик решил окружить березы красной лентой
(зайцы не любят красный цвет и не станут заходить на огражденную лентой территорию).
К сожалению, в его распоряжении оказалась только лента длиной L метров, которую, к тому же, нельзя было разрезать.
Единственное, что можно было делать в этом случае — окружить этой лентой как можно больше берез.
При этом, чтобы сохранить аллею, необходимо окружить на каждой стороне аллеи хотя бы одну березу.
Требуется написать программу, которая по заданной длине ленты, ширине аллеи и положению берез на ней определяет максимальное количество берез,
которое можно окружить этой лентой. Считается, что березы представляются точками, толщиной берез и шириной ленты следует пренебречь.
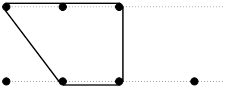
Пояснения к примерам
В первом примере можно, например, оградить березы способом, указанным на рисунке.
Во втором примере длины ленты недостаточно, чтобы оградить хотя бы по одной березе с каждой стороны.
Система оценивания
Правильные решения для тестов, в которых 1 ≤ (N + M) ≤ 50, будут оцениваться из 30 баллов.
Правильные решения для тестов, в которых 1 ≤ (N + M) ≤ 500, будут оцениваться из 60 баллов.
Формат входного файла
Первая строка входного файла содержит два разделенных пробелом целых числа: длину ленты L и ширину аллеи W.
Вторая и третья строки описывают березы вдоль левой стороны аллеи. Вторая строка содержит число N — количество берез, а третья строка содержит N различных целых чисел a1, a2, …, aN, заданных по возрастанию. Четвертая и пятая строки описывают березы вдоль правой стороны аллеи. Четвертая строка содержит число M — количество берез, а пятая строка содержит M различных целых чисел b1, b2, …, bM, заданных по возрастанию.Формат выходного файла
Выходной файл должен содержать одно целое число: максимальное количество берез, которое можно оградить заданной лентой. Гарантируется, что если максимальное число берез, которое можно оградить лентой длины L, равно X, то нет способа оградить (X + 1) березу лентой длины (L + 10−5).
Ограничения
1 ≤ L ≤ 2×105; 1 ≤ W ≤ 104; 1 ≤ N, M ≤ 2000; 0 ≤ ai, bi ≤ 105;
Примеры тестов
| № | Входной файл (birch.in) |
Выходной файл (birch.out) |
|---|---|---|
| 1 |
|
|
| 2 |
|
|