Задача B. Broken chessboard ≡
| Автор: | A. Baranov | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 256 Мб | |
| Выходной файл: | output.txt |
Условие
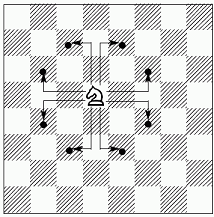 Имеется доска размером n × m клеток, в одной из которых расположен шахматный конь.
При этом часть клеток предварительно была удалена с доски.
Имеется доска размером n × m клеток, в одной из которых расположен шахматный конь.
При этом часть клеток предварительно была удалена с доски.
Требуется определить минимальное число ходов, которое необходимо затратить коню, чтобы последовательно посетить все клетки заданного списка, не проходя при этом через удалённые клетки.
Иными словами, заданный список клеток должен являться подпоследовательностью посещённых конём клеток.
Формат входного файла
Входной файл содержит целые числа n и m — размеры доски.
Далее идёт целое число P, за которым следует P пар целых чисел (ai, bi) — координаты удалённых клеток.
Далее идёт целое число L, за которым следует L пар целых чисел (xi, yi) — координаты клеток, через которые необходимо пройти (включая начальное местоположение коня).
Формат выходного файла
Выходной файл должен содержать единственное целое число — минимальное количество ходов.
Если задача не имеет решения, следует вывести −1.
Ограничения
0 < |xi+1 − xi| + |yi+1 − yi|, 2 ≤ (n, m) ≤ 100,
0 ≤ (ai, xi) < n, 0 ≤ (bi, yi) < m,
0 ≤ P ≤ 5000, 2 ≤ L ≤ 100
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 |
|
|
| 2 |
|
|