Задача Q. Сжатое дерево ≡
| Автор: | А. Баранов | Ограничение времени: | 1 сек | |
| Входной файл: | input.txt | Ограничение памяти: | 16 Мб | |
| Выходной файл: | output.txt |
Условие
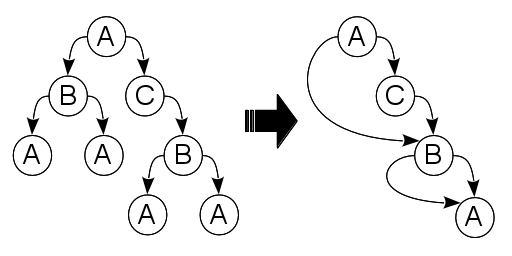
Пусть имеется корневое дерево, узлам которого ранее был приписан определенный набор цветов. Каждый нелистовой узел такого дерева содержит произвольное число ссылок на своих потомков. При этом полагается, что порядок их следования имеет значение.
В исходном дереве могут встречаться поддеревья, обладающие одинаковой структурой. Здесь используется тот факт, что с точки зрения стороннего наблюдателя, два дерева считаются тождественными, если их корни окрашены в одинаковые цвета и все соответствующие потомки тождественны между собой. Как следствие, ссылки на указанные поддеревья также являются взаимозаменяемыми.
Для экономии памяти, исходное дерево следует представить в сжатом виде. С этой целью требуется расставить ссылки на потомков таким образом, чтобы минимизировать число узлов в полученном графе, сохранив при этом структуру исходного дерева.
Формат входного файла
Во входном файле "input.txt" хранится дерево, представленное в следующем виде. Вначале идет цвет корневого узла, после которого (через пробел) указывается число его прямых потомков. Затем следует упорядоченный набор таких потомков, записанных аналогичным образом.
Для обозначения цветов здесь используются цифры и строчные буквы латинского алфавита.
Каждому узлу также ставится в соответствие его порядковый номер (начиная с нуля).
Формат выходного файла
Выходной файл "output.txt" должен содержать пары значений: номер старого узла и номер узла, на который его следует заменить.
При этом корень дерева (узел с нулевым индексом) является не перемещаемым.
В случае если сжатие не может быть выполнено, выходной файл следует оставить пустым.
Ограничения
Полагается, что каждый узел имеет не более 10 потомков.
При этом общее число узлов не превосходит 2 ⋅ 105.
Примеры тестов
| № | Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|---|---|
| 1 | |
|
| 2 | |
|