Задача 7. Красота фейерверка ≡
| Автор: | Центральная предметно-методическая комиссия | Ограничение времени: | 1 сек | |
| Входной файл: | Стандартный вход | Ограничение памяти: | 512 Мб | |
| Выходной файл: | Стандартный выход | |||
| Максимальный балл: | 100 |
Условие
В лаборатории теоретической пиротехники изучают новые технологии организации фейерверков. Фейерверк представляется как корневое дерево, а поскольку в мощном фейерверке его элементы также взрываются, порождая новые фейерверки, то ученые вводят операцию возведения корневого дерева в степень.
Корневое дерево содержит одну или несколько вершин. Одна из вершин выделена и называется корнем дерева, для каждой из остальных вершин ровно одна другая вершина является родителем. При этом от любой вершины можно добраться до корня, последовательно переходя от вершины к ее родителю. Вершина, которая не является родителем никакой другой вершины, называется листом. Если вершина x является родителем вершины y, то вершина y является ребенком вершины x. Будем говорить, что вершина и ее родитель соединены ребром.
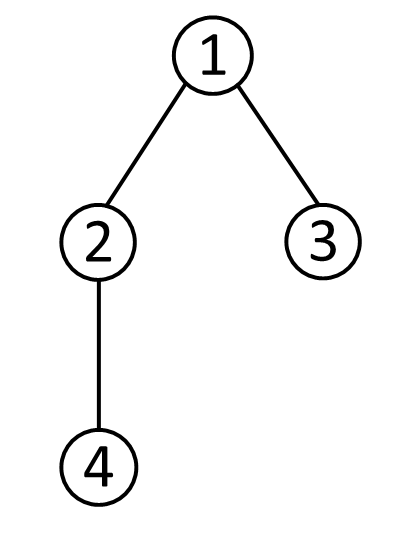
На рис. 1 показан пример корневого дерева с корнем в вершине 1. Родителем вершин 2 и 3 является вершина 1, родителем вершины 4 является вершина 2. Вершины 2 и 3 — дети вершины 1, а вершина 4 — ребенок вершины 2. Листьями являются вершины 3 и 4.
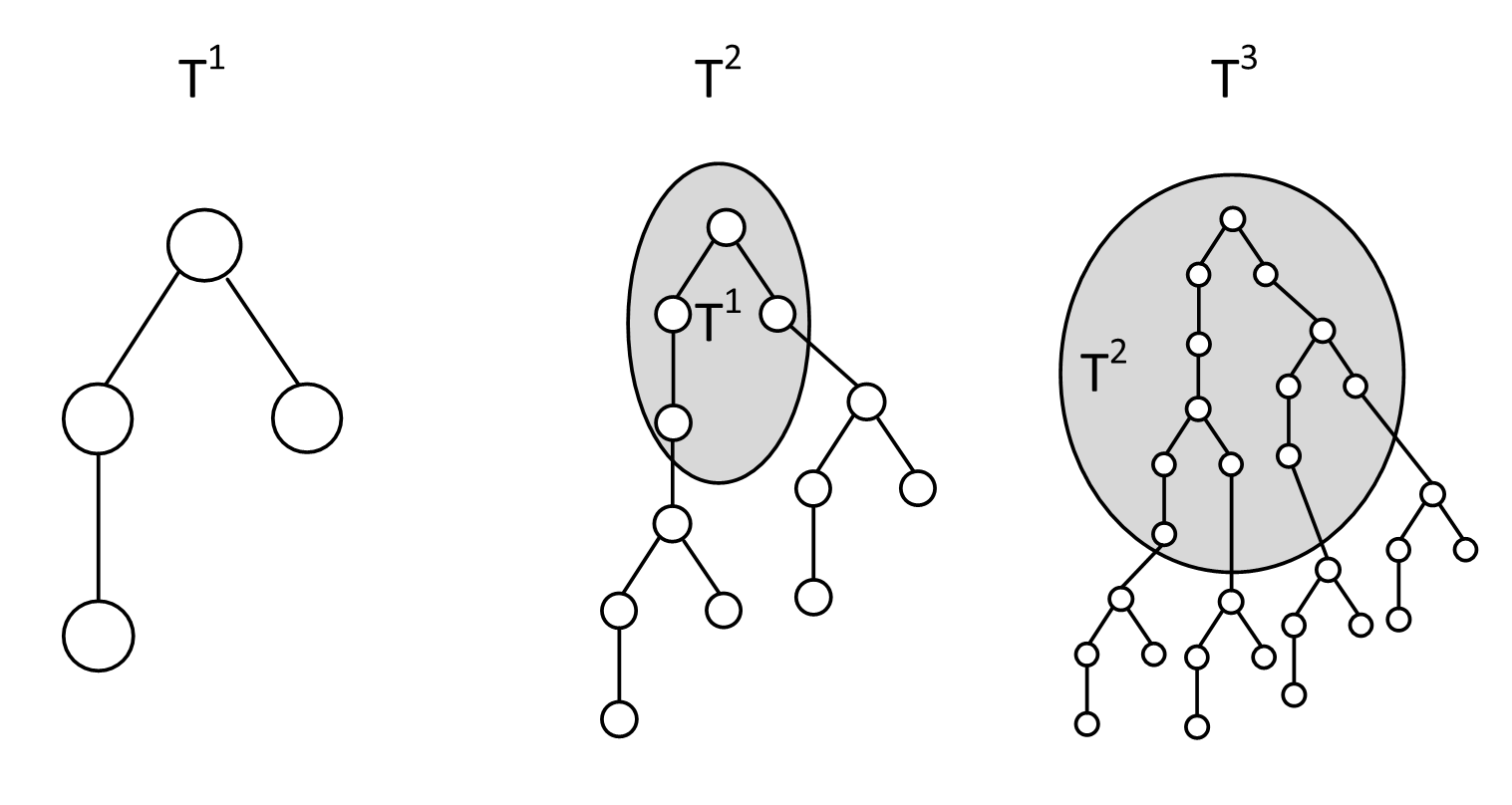
Фейерверк задается своим базовым деревом T и мощностью m. Фейерверк представляется деревом, которое получается в результате возведения дерева T в степень m. Операция возведения дерева в степень устроена следующим образом. Если m = 1, то результат T1 — само дерево T. Для m > 1 рассмотрим дерево Tm − 1. Выполним следующую операцию: для каждого листа x дерева Tm − 1 создадим копию дерева T и назначим лист x родителем корня соответствующей копии. Получившееся дерево будет деревом Tm.
На рис. 2 показано дерево, представленное на рис. 1, в степенях 1, 2 и 3.
Путем в дереве называется последовательность вершин, в которой две соседние вершины соединены ребром. Все вершины в пути должны быть различны.
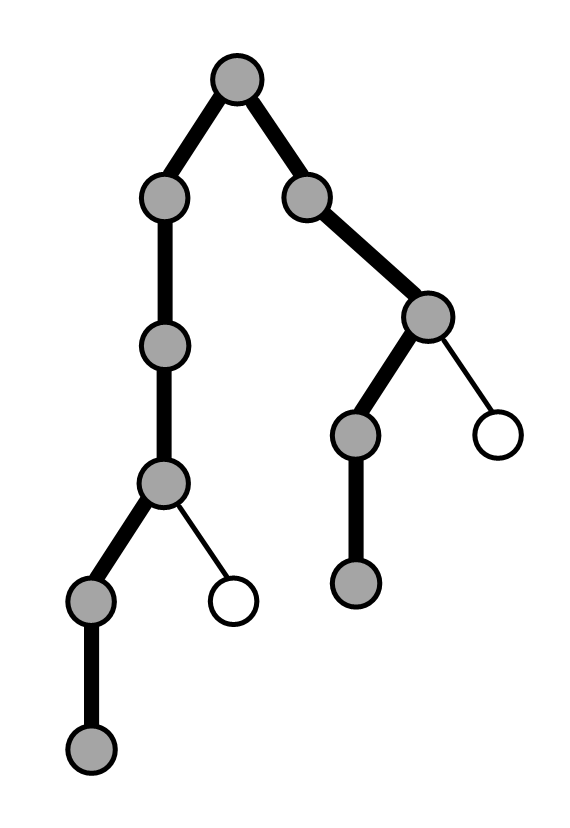
Для того, чтобы оценить красоту фейерверка, необходимо определить, какое максимальное количество вершин может содержать путь в дереве, которым представляется фейерверк. На рис. 3 приведен путь в дереве T2, содержащий максимальное количество вершин. Таким образом, красота фейерверка с базовым деревом T и мощностью 2 равна 10.
Требуется написать программу, которая по описанию дерева T и натуральному числу m определяет красоту фейерверка с базовым деревом T и мощностью m.
Формат входных данных
Первая строка входных данных содержит два натуральных числа n и m — количество вершин в базовом дереве фейерверка T и его мощность.
Вторая строка описывает дерево T и содержит (n − 1) целых чисел: p2, p3, ..., pn — номера родителей вершин 2, 3, ..., n, соответственно.
Формат выходных данных
Требуется вывести одно целое число — красоту фейерверка, представляемого деревом Tm.
Ограничения
3 ≤ n ≤ 200000, 1 ≤ m ≤ 200000
1 ≤ pi ≤ i − 1
Описание подзадач и системы оценивания
Баллы за каждую подзадачу начисляются только в случае, если все тесты для этой подзадачи и необходимых подзадач успешно пройдены.
| Подзадача | Баллы | Дополнительные ограничения | Необходимые подзадачи | Информация о проверке | |
|---|---|---|---|---|---|
| n | m | ||||
| 1 | 19 | 3 ≤ n ≤ 5000 | m = 1 | полная | |
| 2 | 10 | 3 ≤ n ≤ 200000 | m = 1 | 1 | полная |
| 3 | 20 | 3 ≤ n ≤ 5000 | 1 ≤ m ≤ 5000 | 1 | полная |
| 4 | 19 | 3 ≤ n ≤ 5000 | 1 ≤ m ≤ 200000 | 1, 3 | полная |
| 5 | 32 | 3 ≤ n ≤ 200000 | 1 ≤ m ≤ 200000 | 1 — 4 | полная |
Примеры тестов
| № | Стандартный вход | Стандартный выход |
|---|---|---|
| 1 |
|
|