Задача M. Ловушка для подвижных частиц ≡

Условие

В рамках одного научного исследования по изучению псевдо-броуновского движения на плоскости возникла необходимость в моделировании поведения двумерных псевдо-частиц при их попадании в замкнутую ловушку, имеющую форму кольца.

Дело в том, что такого рода частицы в течение всей своей жизни совершают непрерывное прямолинейное движение с некоторой постоянной скоростью. Когда частица сталкивается с каким-либо препятствием, она отклоняется от исходной траектории и продолжает свое движение, как ни в чем не бывало. В очень редких случаях также могут встречаться абсолютно неподвижные частицы, скорости которых равны нулю.

Чтобы изучить подвижную псевдо-частицу, ее необходимо длительное время удерживать в некоторой ограниченной области. Для этого в экспериментальной лаборатории воссоздаются условия при которых достаточно большой набор частиц окажется в пределах замкнутого кольца, граница которого образует силовой барьер, через который частицы не могут пройти.

Определим кольцо, как область, заключенную между двумя окружностями с общим центром (x₀, y₀) и разными радиусами: r₂ > r₁ > 0. В этом случае исходное множество частиц можно условно разбить на три группы:

1. частицы, попадающие во внутренний круг с центром в точке (x₀, y₀) и радиусом r₁ > 0;
2. частицы, заключенные между двумя окружностями с радиусами r₁ и r₂;
3. частицы, лежащие за пределами внешнего круга с радиусом r₂ > r₁.

Рассмотрим поведение указанных частиц на временном интервале от 0 до T.

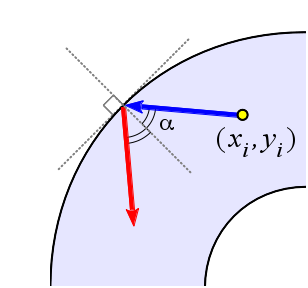
В процессе своего движения каждая отдельно взятая частица может то и дело сталкиваться с границей содержащей ее области. Будем полагать, что при столкновении частицы с границей она отражается относительно касательной прямой (как показано на рисунке). Модуль ее скорости при этом сохраняется. В свою очередь, взаимные столкновения двух и более частиц не влияют на их траектории и могут быть проигнорированы.

Требуется написать программу, которая по известному начальному положению частиц, исходным компонентам скорости и параметрам кольцевой области, производит расчет их траекторий в течение заданного промежутка времени. В качестве ответа вывести координаты положения частиц в равноотстоящие моменты времени t_k = k ⋅ (T / m), где k = 1, 2, …, m.

Важным условием здесь является то, что в процессе движения ни одна из частиц не должна покидать область, которой она принадлежала в начальный момент времени. Данный факт следует также учесть при составлении проверочных тестов.

Формат входного файла

В первой строке входного файла "input.txt" содержатся параметры расчетной области: x₀, y₀, r₁, r₂. Во второй строке указано значение T, задающее длину временного интервала, и число его подынтервалов m. Далее следует натуральное число n и последовательность из 4 × n вещественных чисел, задающих начальные координаты и скорости каждой из частиц: x_i, y_i, u_i, v_i, где i = 1, 2, …, n.

Формат выходного файла

Выходной файл "output.txt" должен содержать координаты положения частиц в моменты времени t_k (k = 1, 2, …, m), расположенные в том же порядке, что и во входном файле. Все значения должны быть указаны с точностью до 5-го знака после запятой.

Ограничения

Полагается, что ни одна из частиц в начальный момент времени не лежит на границе кольца.

2 ≤ r₁ ≤ (r₂ − 2) ≤ 10, 0 < T ≤ 20, 0 < m ≤ 10,

u_i² + v_i² ≤ 25, 0 < n ≤ 4000

Примеры тестов

 1.62400  4.86000  2.01152  4.21450
10.00000  4
 5
 2.24501 -2.75130 -0.46250  1.00000
-1.39080  6.92500  0.02731 -1.75240
-7.10643  2.32470  0.10561  0.27435
 2.07640  4.96800 -0.04658  0.94071
 3.00000  3.75400 -1.04060 -1.04520

 1.08876 -0.25130
-1.32252  2.54400
-6.84240  3.01057
 1.79231  6.39753
 0.09054  3.90417

-0.67633 -0.22719
 2.36153  1.88787
-6.57838  3.69645
 0.85566  4.23718
 1.22695  6.69642

-2.86015 -1.90584
 4.61717  4.01900
-6.31435  4.38232
 1.39629  4.06765
 3.58175  4.57937

-5.04397 -3.58449
 4.04359  7.86965
-6.05033  5.06820
 3.19249  5.59017
 0.69049  3.16606