Задача A. Пересечение двух прямых
Условие
Прямая a проходит через точки A1 (aX1; aY1) и A2 (aX2; aY2).
Прямая b проходит через точки B1 (bX1; bY1) и B2 (bX2; bY2).
Требуется найти точку пересечения прямых a и b или установить что прямые параллельны.
Формат входного файла
Во входном файле содержаться восемь целых чисел — aX1, aY1, aX2, aY2, bX1, bY1, bX2, bY2
Формат выходного файла
Выходной файл должен содержать:
- Единственное число −1, если прямые совпадают;
- Единственное число 0, если прямые параллельны и не имеют общих точек;
-
Два вещественных числа X0, Y0 — координаты точки пересечения прямых с точностью 10−3,
если прямые пересекаются в одной точке;
Ограничения
0 ≤ |aXk|, |aYk|, |bXk|, |bYk| ≤ 105
A1 ≠ A2
B1 ≠ B2
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
0 0 2 2 1 1 3 3
|
-1
|
| 2 |
0 0 1 1
2 3 5 6
|
0
|
| 3 |
1 1
3 5
-1 5
8 -1
|
2.000000000 3.000000000
|
Задача B. Забор Хоттабыча
Условие
Прожив 1000 лет, Гассан Абдуррахман ибн Хоттаб решил заняться изучением математики.
Пройдя тему "Кривые второго порядка", он захотел воспользоваться новыми знаниями на практике,
а заодно вспомнить некоторые магические заклинания.
В результате действий старика появился бесконечный забор, с высоты птичьего полёта
имеющий вид параболы y=ax2+bx+c.
Пока Хоттабыч проводил свой эксперимент, его друг Волька сдавал экзамен по географии.
После появления забора Хоттабыч понял, что забор может отделять Волькину школу от его дома, и
Волька, возможно, больше никогда не сможет попасть домой.
Хоттабыч знает координаты дома Вольки (XH; YH) и координаты школы (XS; YS)
и просит вас подсказать, сможет ли Волька вернуться домой.
Также Хоттабыч знает, что забор не проходит ни через школу, ни через дом Вольки.
Формат входного файла
Во входном файле содержатся целые числа
a b c XH YH XS YS
Формат выходного файла
В выходном файле должно содержаться единственное слово:
YES,
если Волька сможет добраться до дома, или
NO — в противном случае.
Ограничения
Все числа по модулю не превосходят
103.
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
1 0 0
0 1
0 -10
|
NO
|
| 2 |
1 0 0 0 1 0 10
|
YES
|
| 3 |
-2 -8 -16
-1 -11 -4 -17
|
YES
|
Задача C. Пеленг НЛО
Условие
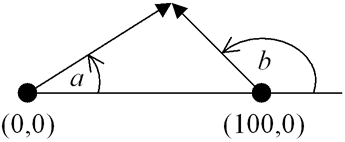
Два радара, расположенные в точках с координатами (0, 0) и (100, 0),
обнаружили неопознанный объект.
По таинственной причине, связанной, возможно, с внеземной природой объекта,
радары оказались способны определить только направление на объект (пеленг),
но не расстояние до объекта.
Пеленг измеряется в градусах, против часовой стрелки,
начиная от направления "на восток"
(т. е. пеленг второго радара относительно первого равен 0°,
пеленг первого радара относительно второго — 180°).
Требуется найти координаты НЛО или определить, что это невозможно.
Формат входного файла
Во входном файле содержатся вещественные числа
a и
b, разделенные пробелами.
Формат выходного файла
В выходном файле должны содержаться два вещественных числа,
x и
y,
представляющие координаты объекта с точностью до 4 знаков после запятой.
Если определить координаты невозможно, следует вывести два числа
0 (нуль).
Ограничения
0 ≤ a, b ≤ 360
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
45.1 135.0
|
49.9127 50.0873
|
| 2 |
135.0 45.0
|
0 0
|
Задача D. Поворот отрезка
Условие
Вершины отрезка AB имеют координаты (Xa; Ya) и (Xb; Yb).
Требуется найти координаты вершин отрезка A* B* (X*a; Y*a) и (X*b; Y*b),
полученного путём поворота отрезка AB вокруг точки O (Xo; Yo) на β градусов.
Формат входного файла
Входной файл содержит целые числа Xa, Ya, Xb, Yb, Xo, Yo, β
Формат выходного файла
Выходной файл должен содержать четыре вещественных числа X*a, Y*a, X*b, Y*b с точностью 10−3.
Ограничения
0 ≤ |Xa|, |Ya|, |Xb|, |Yb|, |Xo|, |Yo| ≤ 105
0 ≤ β ≤ 360
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
1 1 2 2 0 0 90
|
-1.000000000 1.000000000 -2.000000000 2.000000000
|
| 2 |
1 1 2 2
0 0
45
|
0.000000000 1.414213562 0.000000000 2.828427125
|
| 3 |
7 5
11 11
9 8
180
|
11.000000000 11.000000000 7.000000000 5.000000000
|
