Problem D. Database
Statement
Peter studies the theory of relational databases. Table in the relational database
consists of values that are arranged in rows and columns.
There are different normal forms that database may adhere to. Normal forms are
designed to minimize the redundancy of data in the database. For example, a database
table for a library might have a row for each book and columns for book name, book author,
and author's email.
If the same author wrote several books, then this representation is clearly redundant.
To formally define this kind of redundancy Peter has introduced his own normal form.
A table is in Peter's Normal Form (PNF) if and only if there is no pair of
rows and a pair of columns such that the values in the corresponding columns are the
same for both rows.
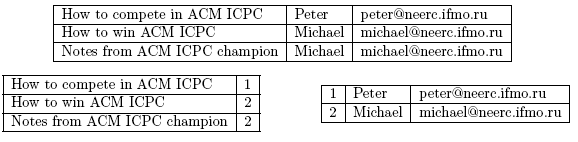
The first table is clearly not in PNF, since values for 2rd and 3rd columns repeat in 2nd and 3rd rows.
However, if we introduce unique author identifier and split this table into two tables — one containing book name
and author id, and the other containing book id, author name, and author email, then both
resulting tables will be in PNF.
Given a table your task is to figure out whether it is in PNF or not.
Input file format
The first line of the input file contains two integer numbers n and m (1 ≤ n ≤ 10 000,
1 ≤ m ≤ 10), the number of rows and columns in the table.
The following n lines contain table rows. Each row has m column values separated by commas.
Column values consist of ASCII characters from space (ASCII code 32) to tilde (ASCII code 126)
with the exception of comma (ASCII code 44). Values are not empty and have no leading and trailing
spaces. Each row has at most 80 characters (including separating commas).
Output file format
If the table is in PNF write to the output file a single word "YES" (without quotes). If the table is not in PNF,
then write three lines. On the first line write a single word "NO" (without quotes). On the second line write
two integer row numbers r1 and r2 (1 ≤ r1, r2 ≤ n, r1 ≠ r2), on the third line write two
integer column numbers c1 and c2 (1 ≤ c1, c2 ≤ m, c1 ≠ c2), so that values in columns
c1 and c2 are the same in rows r1 and r2.
Sample tests
| No. |
Input file (database.in) |
Output file (database.out) |
|---|
| 1 |
3 3
How to compete in ACM ICPC,Peter,peter@neerc.ifmo.ru
How to win ACM ICPC,Michael,michael@neerc.ifmo.ru
Notes from ACM ICPC champion,Michael,michael@neerc.ifmo.ru
|
NO
2 3
2 3
|
| 2 |
2 3
1,Peter,peter@neerc.ifmo.ru
2,Michael,michael@neerc.ifmo.ru
|
YES
|
Problem F. Funny Language
Statement
There is a well know game with words. Given a word you have to write as many
other words as possible using the letters from the given word. If the letter
repeats multiple times in the original word, you can use it up to as many times
in the new words. The order of letters in the original word does not matter.
For example, given the word CONTEST you can write NOTE, NET, ON, TEST, SET, etc.
Now you are in charge of writing a new dictionary. Your task is to sneak n
new words into it. You know in advance m words Wi (1 ≤ i ≤ m)
that you will have to play a game with and you need to figure out which new n words
to add to the dictionary to maximize the total number of words you can
write out of these m words.
More formally, find such a set of nonempty words S where |S| = n,
Wi ∉ S for any i, and ∑1 ≤ i ≤ m|Si| is maximal, where
Si ⊂ S is the set of words that can be written using
letters from Wi.
Input file format
The first line of the input file contains two integer numbers n
(1 ≤ n ≤ 100) — the number of new words you can add to the
dictionary and m (1 ≤ m ≤ 1 000) — the number of words you will
play the game with. The following m lines contain original words.
Each word consists of at most 100 uppercase letters from A to Z.
Output file format
Write to the output file n lines with a new word on a line.
Sample tests
| No. |
Input file (funny.in) |
Output file (funny.out) |
|---|
| 1 |
3 5
A
ACM
ICPC
CONTEST
NEERC
|
C
CN
E
|
Problem J. Java Certification
Statement
You have just completed Java Certification exam that contained n questions.
You have a score card that explains your performance. The example of the scorecard
is given below.

From this scorecard you can infer that the questions are broken down into m categories
(in the above example m = 6). Each category contains ni questions (1 ≤ ni ≤ n),
so that ∑1 ≤ i ≤ m ni = n. You know that you have correctly answered
k questions out of n (in the above example k = 78 and n = 87),
so you can easily find the number of incorrect answers w = n − k
(in the above example w = 9).
You do remember several questions that you were unsure about and you can guess what category
they belong to. To figure out if your answers on those questions were right or wrong,
you really want to know how many incorrect answers you have given in each category.
Let wi (0 ≤ wi ≤ ni) be the number of incorrect answers in i-th category, ∑1 ≤ i ≤ m wi = w.
From the scorecard you know the percentage of correct answers in each category.
That is, for each i from 1 to m you know the value of 100(ni − wi) / ni
rounded to the nearest integer. The value with a fractional part of 0.5 is
rounded to the nearest even integer.
It may not be possible to uniquely find the valid values for wi. However, you
guess that the questions are broken down into categories in a mostly uniform manner.
You have to find the valid values of wi and ni, so that to minimize the difference
between the maximum value of ni and the minimum value of ni. If there are still
multiple possible values for wi and ni, then find any of them.
Input file format
The first line of the input file contains three integer numbers — k, n, and m,
where k (0 ≤ k ≤ n) is the number of correctly answered questions,
n (1 ≤ n ≤ 100) is the total number of questions, m (1 ≤ m ≤ 10)
is the number of question categories. The following m lines of the input file
contain one integer number from 0 to 100 (inclusive) on a line —
percentages of the number of the correct answers in each category.
The input file always corresponds to some valid set of wi and ni.
Output file format
Write to the output file m lines with two integer numbers wi and ni on a line,
separated by a space — the number of incorrect answers and the total number of questions
in each category, satisfying constraints as given in the problem statement.
Sample tests
| No. |
Input file (javacert.in) |
Output file (javacert.out) |
|---|
| 1 |
78 87 6
100
100
83
92
75
93
|
0 13
0 13
3 18
1 13
4 16
1 14
|

