Задача A. Задача Пифагора
Условие
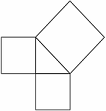
Пифагор заказал ремесленнику изготовить несколько прямоугольных треугольников
из ценных пород дерева для использования на занятиях по геометрии,
но ремесленник перепутал размеры, и треугольники получились не прямоугольные.
Чтобы не выбрасывать испорченный ценный материал,
ремесленник решил переделать получившиеся треугольники в прямоугольные,
постаравшись максимизировать их площади.
Напишите программу, которая по размерам сторон треугольника
находит максимальную площадь прямоугольного треугольника,
который можно вырезать из этого треугольника.
Формат входного файла
В первой строке входного файла содержится три числа,
разделенных пробелами — длины сторон треугольника.
Формат выходного файла
В первой строке выходного файла вывести
одно число — максимальную площадь прямоугольного треугольника,
получаемого из заданного треугольника, с точностью
10−5.
Ограничения
Все числа вещественные, больше 0 и меньше 1000.
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
10.0 10.0 10.0
|
25.00000
|
Задача B. Кольцевая автодорога
Условие
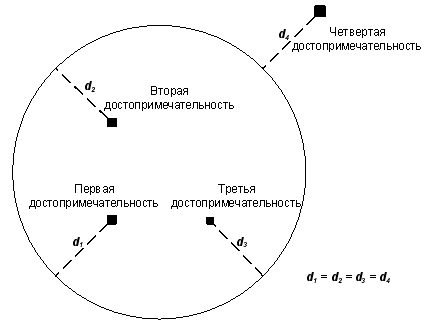
К 2110 году город Флэтбург, являясь одним из крупнейших городов мира, не имеет обходной автомагистрали,
что является существенным препятствием для его развития как крупнейшего транспортного центра мирового значения.
В связи с этим еще в 2065 году при разработке Генерального плана развития Флэтбурга была определена необходимость
строительства кольцевой автомобильной дороги.
В Генеральном плане также были обозначены требования к этой дороге. Она должна соответствовать статусу кольцевой —
иметь форму окружности. Кроме этого, четыре крупные достопримечательности Флэтбурга должны быть в одинаковой
транспортной доступности от дороги. Это предполагается обеспечить тем, что они будут находиться на равном расстоянии
от нее. Расстоянием от точки расположения достопримечательности до дороги называется наименьшее из расстояний
от этой точки до некоторой точки, принадлежащей окружности автодороги.
Дирекция по строительству города Флэтбурга, ответственная за постройку кольцевой автодороги, решила привлечь передовых
программистов для выбора оптимального плана постройки дороги.
Требуется написать программу, которая вычислит число возможных планов постройки кольцевой автомобильной дороги с
соблюдением указанных требований и найдет такой план, для которого длина дороги будет минимальной.
Формат входного файла
Входной файл содержит четыре строки. Каждая из них содержит по два целых числа: xi и yi — координаты места
расположения достопримечательности. Первая строка описывает первую достопримечательность, вторая — вторую,
третья — третью, четвертая — четвертую. Никакие две достопримечательности не находятся в одной точке.
Формат выходного файла
В первой строке выходного файла требуется вывести число возможных планов постройки кольцевой автомобильной дороги.
Если таких планов бесконечно много, необходимо вывести в первой строке выходного файла слово Infinity.
На второй строке требуется вывести координаты центра дороги минимальной длины и ее радиус. Если существует несколько
разных способов построения дороги минимальной длины, необходимо вывести координаты центра и радиус любой из них.
Координаты центра и радиус дороги должны быть выведены с точностью не хуже 10−8
и не превосходить по абсолютной величине 109.
Ограничения
−100 ≤ xi, yi ≤ 100
Примеры тестов
| № |
Входной файл (road.in) |
Выходной файл (road.out) |
|---|
| 1 |
0 0
0 1
1 0
2 2
|
7
1.5 0.5 1.14412281
|
| 2 |
0 0
0 1
1 0
1 1
|
Infinity
0.5 0.5 0.0
|
Задача C. Нечётный N-угольник
Условие
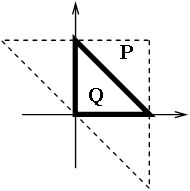 Выпуклый N-угольник P преобразуется в N-угольник Q путём замены
середин сторон исходного многоугольника P на вершины многоугольника Q.
Требуется по выпуклому N-угольнику Q,
заданному координатами вершин, восстановить координаты
вершин исходного N-угольника P.
Выпуклый N-угольник P преобразуется в N-угольник Q путём замены
середин сторон исходного многоугольника P на вершины многоугольника Q.
Требуется по выпуклому N-угольнику Q,
заданному координатами вершин, восстановить координаты
вершин исходного N-угольника P.
Формат входного файла
Входной файл содержит
нечётное число вершин
N,
за которым следуют целочисленные координаты
xi yi вершин многоугольника
Q,
перечисленные в порядке обхода по часовой стрелке.
Значения координат находятся в диапазоне от
−20000 до
20000.
Все числа во входном файле целые и разделены произвольным
количеством пробелов и/или символов перевода строки.
Формат выходного файла
В выходном файле должны содержаться координаты вершин
N-угольника
P,
перечисленные в порядке обхода по часовой стрелке.
При этом первая и вторая вершина должны образовывать сторону,
на которой лежит первая вершина
N-угольника
Q.
Ограничения
3 ≤ N ≤ 999.
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
3
0 0
0 1
1 0
|
1 -1
-1 1
1 1
|
Problem D. Eye of the Admin
Statement
Young system administrator Vasya is moving into a new server room.
The room has a shape of convex polygon with LCD monitors
mounted on some of the walls.
Monitors display the health data of various servers, so Vasya
wishes to place his rotating chair such that he could observe
them all without need to leave it.
 He moved all obstacles out of the way, so he can see any point
of any monitor from any place inside the room.
The only problem is that the image on LCD monitors deteriorates at
large viewing angles.
He moved all obstacles out of the way, so he can see any point
of any monitor from any place inside the room.
The only problem is that the image on LCD monitors deteriorates at
large viewing angles.
Viewing angle is an angle between the line connecting the eye of viewer
with the point on monitor and the normal vector at that point.
The angle can have values in range from 0 to π / 2.
Vasya wants to place his chair at
a point which minimizes a maximum viewing angle from him to any point
of any monitor.
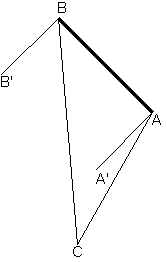
For example, in a picture line segment AB represents a monitor,
point C — a chair, angles A'AC and B'BC are viewing angles,
and the second of them is the maximum one.
Input file format
Input file contains the number of monitors N followed by N triplets of integers
xi yi ai, where xi yi — coordinates of room vertexes in counter-clockwise order,
ai = 1 if the wall between the i-th vertex and the next one is covered by a monitor,
ai = 0 otherwise.
Output file format
Output file must contain floating point values x y —
coordinates of point to place a chair. The point must lie inside the room.
If there is more than one solution, output any of them.
The maximum viewing angle from point (x, y) must differ
from the correct answer by at most 10−3 (measured in radians).
Constraints
3 ≤ N ≤ 40,
1 ≤ Σ ai ≤ 10,
0 ≤ xi, yi ≤ 105.
Sample tests
| No. |
Input file (input.txt) |
Output file (output.txt) |
|---|
| 1 |
4
0 0 1
10 0 0
10 10 1
0 10 0
|
5.0 5.0
|


 Выпуклый
Выпуклый  He moved all obstacles out of the way, so he can see any point
of any monitor from any place inside the room.
The only problem is that the image on LCD monitors deteriorates at
large viewing angles.
He moved all obstacles out of the way, so he can see any point
of any monitor from any place inside the room.
The only problem is that the image on LCD monitors deteriorates at
large viewing angles.