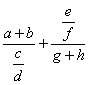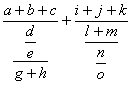Задача A. Дробь в LATeX-е
Условие
Издательская система LATeX предназначена для верстки сложных научно-технических текстов
с большим количеством формул. Исходный файл для системы LATEX пишется на языке TEX и
представляет собой текст документа, в который включены специальные символы и команды.
Специальные символы и команды описывают размещение текста, в частности в математических формулах.
Команда представляет собой последовательность латинских букв (регистр важен), перед которой
стоит символ "\". Так, команда \frac предназначена для описания дроби, в которой числитель
расположен над знаменателем. Рассмотрим простейшую структуру команды \frac.
Комадна \frac имеет два параметра - числитель и знаменатель.
Перед самой командой не обязательно ставить пробел.
Следом за ключевым словом \frac записываются числитель и знаменатель.
Если числитель и знаменатель имеют длину более одного символа, они заключаются в фигурные скобки.
Если числитель или знаменатель записываются одной буквой или цифрой, их можно не брать в фигурные скобки.
Если числитель записывается одним символом, то он отделяется от \frac хотя бы одним пробелом.
Если знаменатель записывается одним символом, то он не отделяется пробелом от числителя.
Произвольное ненулевое количество пробелов считается синтаксически эквивалентным одному пробелу.
Нельзя разделять пробелами на части ключевое слово \frac.
Дадим также формальное определение выражения для нашей задачи:
- <выражение> ::= <элемент> | <элемент> <выражение>
- <элемент> ::= <дробь> | "{" <выражение> "}" | <другой математический элемент>
- <дробь> ::= "\frac" <тело дроби>
- <тело дроби> ::= <числитель><знаменатель>
- <числитель> ::= <пробелы><непробельный символ> | [<пробелы>] "{" <выражение> "}"
- <знаменатель> ::= <непробельный символ> | [<пробелы>] "{" <выражение> "}"
- <другой математический элемент> ::= произвольная последовательность печатных символов, не содержащая фигурных скобок и подстроки "\frac"
- <пробелы> ::= " " | " " <пробелы>
- <непробельный символ> ::= произвольный печатный символ, за исключением " ", "\", "{" и "}"
Здесь вертикальная черта | означает "или", заключенная в квадратные скобки часть может отсутствовать,
а символы, записаные в кавычках обозначают самих себя.
Печатный символ - любой символ с ASCII кодом от 32 (пробел) до 127.
Например, выражение
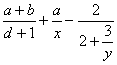
записывается на языке TEX как
\frac{a+b}{d+1}+\frac ax -\frac 2 {2+\frac{3}{y}}
Чтобы в печатаемом документе вывести формулу, необходимо вычислить ее высоту для используемого
при печати шрифта. Шрифт определяет размеры S - высоту отдельного символа и D - высоту горизонтальной
дробной черты. Значения S и D задаются целыми числами.
Ваша задача - для заданного выражения на языке TEX вычислить высоту формулы.
Отметим, что если две дроби принадлежат одному выражению,
то их дробные черты записываются на одном уровне, а если нет
(например, относятся к числителям или знаменателям различных дробей),
это свойство может и не выполняться. Чтобы проиллюстрировать применение этого правила, приведем два примера:
\frac{a+b}{\frac cd}+\frac{\frac ef}{g+h} |
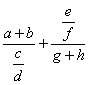 |
\frac{a+b+c}{\frac{\frac de}{g+h}}+\frac{i+j+k}{\frac{l+m}{\frac no}} |
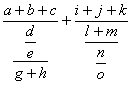 |
Формат входного файла
В первой строке находятся целые положительные числа
S и
D.
Следующая строка содержит описание формулы на TEX-е, длина строки не более 200 символов.
Гарантируется, что формула синтаксически корректна, то есть фигурные скобки образуют
правильную скобочную последовательность и строка содержит только печатные символы.
Все символы "\", встречающиеся в строке относятся к некоторой командной последовательности
(не обязательно \frac), можете считать, что все прочие командные последовательности задают символы,
высота которых равна
S. Числитель и знаменатель каждой дроби содержат хотя бы по одному символу,
вся формула содержит хотя бы один символ.
Формат выходного файла
Выведите в выходной файл единственное число — высоту формулы.
Ограничения
1 ≤
S,
D ≤ 10000
Примеры тестов
| № |
Входной файл (frac.in) |
Выходной файл (frac.out) |
|---|
| 1 |
10 2
\frac{a+b}{d+1}+\frac ax -\frac 2 {2+\frac{3}{y}}
|
34
|
| 2 |
10 2
no fractions here
|
10
|
| 3 |
10 2
\frac {\alpha} {\beta+\sin{2+x}}
|
22
|
| 4 |
10 2
\cos{\frac{\alpha}b}
|
22
|
| 5 |
10 2
\frac a {sin{a}}
|
22
|
| 6 |
10 2
\frac{a+b}{\frac cd}+\frac{\frac ef}{g+h}
|
46
|
| 7 |
10 2
\frac{a+b+c}{\frac{\frac de}{g+h}}+\frac{i+j+k}{\frac{l+m}{\frac no}}
|
46
|
Problem B. Code Formatting
Statement
Programmers are known to wage religious wars when issues of proper
code formatting are discussed. When new team of programmers starts working
on a project, it often brings slightly different code
formatting style and wants to reformat old source code according to
their own style. Moreover, inexperienced programmers often neglect the
importance of good and consistent code style, thus complicating the
work of their teammates and themselves. This situation creates thriving
market for code formatting tools.
You are taking part in a proof-of-concept project for a new code formatting
tool code named Salvation. This is only a pilot project aimed not for
a practical usefulness, but to demonstrate your ability to parse and format
code of a high-level language. Your task is to write code formatter for a
language called TRIVIAL (The Rival Implementation-Agnostic Language).
This language has trivial lexical and grammatical structures.
It does not have any keywords and control structures, because all
constructs of the language are represented as function calls and closures.
The lexical structure consists of identifiers, opening and closing parenthesis
and curly braces, commas, and semi-colons. Identifiers consist only of
digits '0'--'9' and Latin letters 'a'--'z', 'A'--'Z'.
Lexical terms may be separated by whitespaces, leading and trailing whitespaces in
the file are also allowed. Whitespace may consist of spaces,
tab characters (ASCII code 9), and line separators (a pair of ASCII 13, 10).
The structure of the valid trivial program is derived from the following productions:
- Program ::= Block
- Block ::= '{' Statements '}'
- Statements ::= Statement | Statement Statements
- Statement ::= Expression ';'
- Expression ::= identifier ['(' Arguments ')'] [Block]
- Arguments ::= Expression | Expression ',' Arguments
Properly formatted trivial program additionally conforms to the following rules:
- There are no empty lines.
- Tab characters are not used.
- The first character of the file is opening curly brace '{' (no preceding whitespaces),
and the last character of the file is closing curly brace '}' (no trailing whitespaces).
- Each line is preceded by 4N space characters, where N is called indentation level.
- The first and the last lines of the program have zero indentation level.
- Lines that constitute block body and are enclosed in curly braces '{'…'}'
have one more indentation level.
- No whitespace is allowed inside the line with the exception of the following
two cases where a single space character is mandatory: before opening curly brace
character '{' and after comma ','.
- Lines (with the only exception of the last line) end with
semicolon ';' or opening curly brace '{' characters. These
characters cannot appear in the middle or at the beginning of any line
(including the last one).
- Closing curly brace '}' characters appear only at the beginning of lines
after indentation spaces.
See sample output section for an example of properly formatted trivial program.
Input file format
The input file contains valid trivial program.
Output file format
Write to the output file properly formatted trivial code for the program given in the input file.
Constraints
Size of the input file does not exceed 2000 bytes.
Sample tests
| No. |
Input file (code.in) |
Output file (code.out) |
|---|
| 1 |
{class(Point)
{
member ( int ( x ) ) ; member ( int ( y ) ) ;
member ( fun ( Length )
{
return ( sqrt ( sum ( sqr ( x ),sqr ( y ) ) ) );
} ) ;
};
Main
{
repeat
{
set ( n,input ( int ) ) ;
for ( int ( i,0 ) , lt ( i,n ) , inc ( i ) )
{
print ( mult ( n,n ) ) ;
};
};
}; }
|
{
class(Point) {
member(int(x));
member(int(y));
member(fun(Length) {
return(sqrt(sum(sqr(x), sqr(y))));
});
};
Main {
repeat {
set(n, input(int));
for(int(i, 0), lt(i, n), inc(i)) {
print(mult(n, n));
};
};
};
}
|
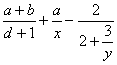 записывается на языке TEX как
записывается на языке TEX как