Problem A. Repeating digit (easy)
Statement
For given integers P and N you need to find all
such values of x < 10N,
that N last digits of xP are non-zero and equal.
Fortunately, there is not so many numbers showing this property.
For example, for P = 2 and N = 2 there exist only 4 of
them:
12, 38, 62, 88
Input file format
Input file contains
P and
N.
Output file format
Output the number of existing numbers X, then all these numbers in any order.
Constraints
2 ≤ P ≤ 100
2 ≤ N ≤ 9
Sample tests
| No. |
Input file (input.txt) |
Output file (output.txt) |
|---|
| 1 |
3 2
|
8
14 42 53 64 77 71 92 99
|
Problem B. Very Simple Problem
Statement
During a preparation of programming contest, its jury is usually faced with many difficult tasks. One of them is to select a problem simple enough to most, if not all, contestants to solve.
The difficulty here lies in diverse meanings of the term "simple" amongst the jury members. So, the jury uses the following procedure to reach a consensus: each member weights each proposed problem with a positive integer "complexity rating" (not necessarily different for different problems). The jury member calls "simplest" those problems that he gave the minimum complexity rating, and "hardest" those problems that he gave the maximum complexity rating.
The ratings received from all jury members are then compared, and a problem is declared as "very simple", if it was called as "simplest" by more than a half of the jury, and was called as "hardest" by nobody.
Input file format
The first line of input file contains integers N and P, the number of jury members and the number of problems. The following N lines contain P integers in range from 0 to 1000 each - the complexity ratings.
Output file format
Output file must contain an ordered list of "very simple" problem numbers, separated by spaces. If there are no such problems, output must contain a single integer 0 (zero).
Constraints
1 ≤ N, P ≤ 100
Sample tests
| No. |
Input file (input.txt) |
Output file (output.txt) |
|---|
| 1 |
4 4
1 1 1 2
5 900 21 40
10 10 9 10
3 4 3 5
|
3
|
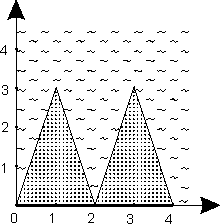
Problem C. Beach cut
Statement
The seashore is represented by a polyline without self-intersections, described by
a sequence of vertices (x1, y1), … (xN, yN).
It also has a property that xi < xi + 1.
The sea is above the line, and the beach — below.
Your program must connect two vertices with a straight line not longer than L
chosen so as to maximize the beach area enclosed between that line and the shore.
The line must not intersect with the sea and may only touch, not intersect,
the shore polyline.
Input file format
Input file contains integer numbers
N L,
followed by
N pairs of integers
x1 y1… xN yN.
Output file format
Output file must contain a single floating point value — the maximum area that can be cut (it may be zero).
The area must be output
exactly, i.e. without any rounding at all.
Constraints
3 ≤ N ≤ 5000,
0 ≤ xi, yi, L ≤ 1000000
Sample tests
| No. |
Input file (input.txt) |
Output file (output.txt) |
|---|
| 1 |
5 4
0 0 1 3 2 0 3 3 4 0
|
6
|
| 2 |
3 10
100 100 101 0 102 100
|
0
|
