Задача A. Хоттабыч и гирлянда ≡

Автор:А. Жуплев
Входной файл: input.txt   Ограничение времени:2 сек
Выходной файл: output.txt   Ограничение памяти:64 Мб
Максимальный балл:100  

Условие

Однажды под новый год Гассан Абдуррахман ибн Хоттаб решил помочь Вольке нарядить ёлку. Среди ёлочных украшений Хоттабычу больше всего понравилась гирлянда, состоящая из N цветных лампочек. Приглядевшись, Хоттабыч насчитал K различных цветов лампочек.

Хоттабыч вспомнил два своих любимых цвета, нашел пару ближайших друг к другу лампочек первого и второго цветов (порядок лампочек в паре не имеет значения), и подсчитал количество лампочек между ними. Потом он выбрал ещё два цвета и повторил поиск для них... Хоттабычу очень понравилось это занятие, и теперь он просит вас написать программу, которая, получив на входе описание гирлянды и M запросов Хоттабыча, отвечала бы на каждый запрос.

Рекомендуется рассмотреть частичные решения

Формат входного файла

В первой строке входного файла содержится число N.

В последующих N строчках содержатся цвета лампочек гирлянды.

В N+2-й строке входного файла содержится число M.

В последующих 2*M строчках содержатся запросы Хоттабыча (по две строки на запрос).

Формат выходного файла

Выходной файл должен содержать M чисел — ответы для каждого запроса в порядке поступления.

Если в запросе указан цвет, отсутствующий на гирлянде, то в качестве ответа следует вывести −1.

Если лампочки обоих цветов есть, но пару найти невозможно, следует вывести −2.

Ограничения

2 ≤ N ≤ 15000

1 ≤ M ≤ 20000

1 ≤ K ≤ 3000

Строка, задающая цвет, состоит из латинских букв, её длина не превышает 255 символов.

Примеры тестов

№ Входной файл (input.txt) Выходной файл (output.txt)
1 
10
Red
Green
Blue
Red
Brown
Green
Yellow
Black
Green
Red
6
Red
Green
Blue
Brown
Yellow
Green
Red
Black
Black
Blue
Orange
Green
 
0
1
0
1
4
-1
2 
10
B
C
D
F
G
E
R
C
A
G
3
C
G
R
B
E
E
 
1 5 -2

Задача B. Чебурашка и бильярд ≡

Автор:А. Жуплев
Входной файл: input.txt   Ограничение времени:1 сек
Выходной файл: output.txt   Ограничение памяти:64 Мб
Максимальный балл:100  

Условие

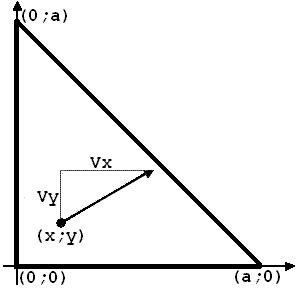Чебурашка учится играть в бильярд и тренируется точно отражать шарик от бортика. Для этого он соорудил тяжёлую рамку в виде равнобедренного прямоугольного треугольника с катетами длиной a. Чебурашка расположил рамку так, что прямой угол совпадает с началом координат, а катеты лежат на положительных направлениях осей.

Затем Чебурашка установил бильярдный шарик внутрь рамки, в точку с координатами (x; y) и ударил по нему, в результате чего шарик начал двигаться с вектором скорости (Vx; Vy). Шарик движется без трения, т.е. скорость шарика не уменьшается со временем. При ударе об один бортик шарик отскакивает без потери скорости под углом, равным углу падения. Если шарик ударяется сразу о два бортика (т.е. попадает точно в угол), то вектор его скорости меняет направление на противоположное. Чебурашке интересно, какие координаты будет иметь шарик через время t, и он просит вас написать программу, отвечающую на этот вопрос.

Диаметр шарика пренебрежимо мал по сравнению с a.

Рекомендуется рассмотреть частичные решения

Формат входного файла

Во входном файле содержится целое число a, за которым следуют вещественные числа x y Vx Vy t, заданные с точностью 10−5

Формат выходного файла

В выходном файле должно содержаться два числа — координаты (Xt; Yt) шарика через время t, выведенные с точностью не менее 10−3

Ограничения

1 ≤ a ≤ 103, 0 ≤ |Vx|, |Vy| ≤ 103, 0 ≤ t ≤ 106

Примеры тестов

№ Входной файл (input.txt) Выходной файл (output.txt)
1 
4 0 0 0.01 0.01 300
 
1.000 1.000
2 
5 2 1 -1 3 2
 
0.000 3.000
3 
10 1 1 -200 -1000 6891.99971
 
1.058 1.290

Задача C. Алгоритм Евклида ≡

Автор:Рекомендации жюри Всероссийской олимпиады
Входной файл: input.txt   Ограничение времени:2 сек
Выходной файл: output.txt   Ограничение памяти:64 Мб
Максимальный балл:50  

Условие

Дима недавно начал изучать информатику. Одним из первых алгоритмов, который он изучил, был алгоритм Евклида для нахождения наибольшего общего делителя (НОД) двух чисел. Напомним, что наибольшим общим делителем двух чисел a и b называется наибольшее натуральное число x, такое, что и число a, и число b делится на него без остатка.

Алгоритм Евклида заключается в следующем:

  1. Пусть a, b — числа, НОД которых надо найти.
  2. Если b = 0, то число a — искомый НОД.
  3. Если b > a, то необходимо поменять местами числа a и b.
  4. Присвоить числу a значение a − b.
  5. Вернуться к шагу 2.
Дима достаточно быстро освоил алгоритм Евклида и вычислил с его помощью много наибольших общих делителей. Наконец, ему пришла идея решить новую задачу. Пусть заданы числа a, b, c и d. Требуется узнать, наступит ли в процессе реализации алгоритма Евклида для заданной пары чисел (a, b) такой момент, когда перед исполнением шага 2 число a будет равно c, а число b будет равно d.

Рекомендуется рассмотреть частичные решения

Формат входного файла

Первая строка входного файла содержит количество наборов входных данных k. Далее идут описания этих наборов. Каждое описание состоит из двух строк. Первая из них содержит два целых числа a b, а вторая — два целых числа: c d.

Формат выходного файла

Для каждого набора входных данных выведите в отдельной строке выходного файла слово "YES", если в процессе применения алгоритма Евклида к паре чисел (a, b) в какой-то момент получается пара (c, d), или слово "NO" в противном случае.

Ограничения

1 ≤ k ≤ 100, 1 ≤ a, b, c, d ≤ 1018

Примеры тестов

№ Входной файл (input.txt) Выходной файл (output.txt)
1 
2
20 10
10 10
10 7
2 4
 
YES
NO
0.051s 0.008s 13