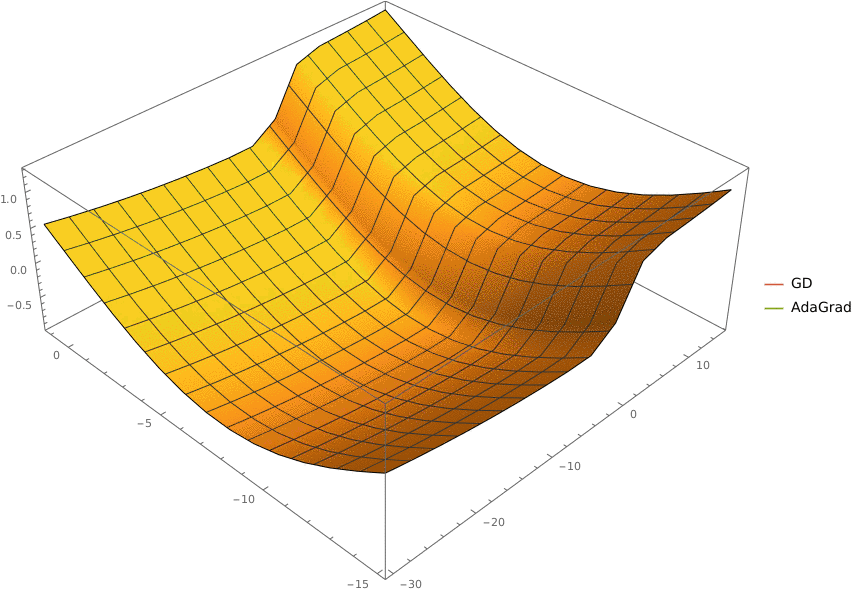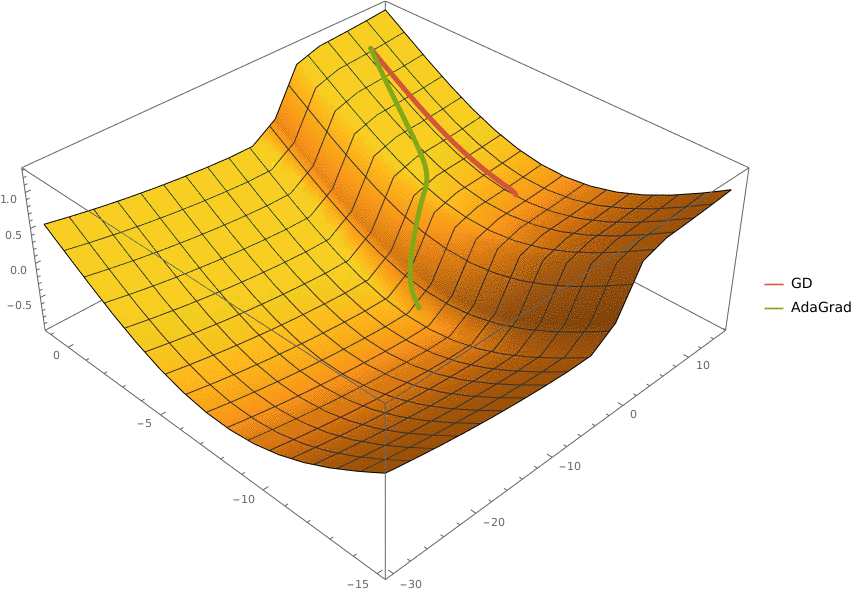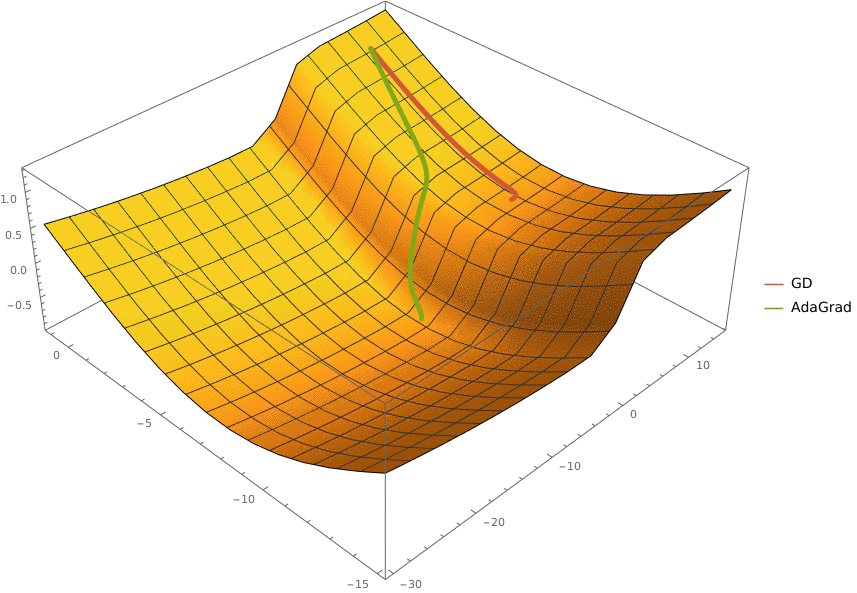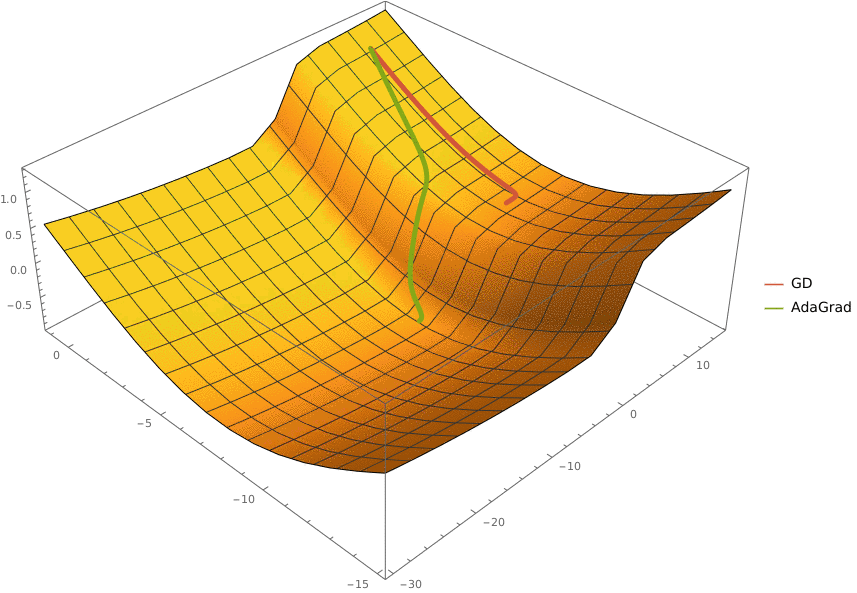
Задача A. Градиентный спуск ≡

Условие

Требуется реализовать класс на языке Python, который соответствует следующему интерфейсу.

class GradientOptimizer: def __init__(self, oracle, x0): self.oracle = oracle self.x0 = x0 def optimize(self, iterations, eps, alpha): pass

В конструктор принимаются два аргумента — оракул, с помощью которого можно получить градиент оптимизируемой функции, а также точку, с которой необходимо начать градиентный спуск.

Метод optimize принимает максимальное число итераций для критерия остановки, L2-норму градиента, которую можно считать оптимальной, а также learning rate. Метод возвращает оптимальную точку.

Оракул имеет следующий интерфейс:

class Oracle: def get_func(self, x): pass def get_grad(self, x): pass

x имеет тип np.array вещественных чисел.

Формат выходных данных

Код должен содержать только класс и его реализацию. Он не должен ничего выводить на экран.

Задача B. Gradient Descent with Momentum ≡

Условие

Требуется реализовать на языке Python класс GDM, который описывает алгоритм градиентного спуска с моментом и имеет следующий интерфейс:

Параметрами алгоритма являются:

• alpha — скорость затухания момента,
• eta — learning rate.

• oracle — оптимизируемая функция,
• x0 — начальная точка,
• max_iter — максимальное количество итераций,
• eps — пороговое значение L2 нормы градиента.

Класс Oracle описывает оптимизируемую функцию:

Формат выходных данных

Код решения должен содержать только определение и реализацию класса.

Задача C. Nesterov Accelerated Gradient ≡

Условие

Требуется реализовать на языке Python класс NesterovAG, который описывает алгоритм ускоренного градиента Нестерова и имеет следующий интерфейс

import numpy as np

class NesterovAG:
    '''Represents a Nesterov Accelerated Gradient optimizer

    Fields:
        eta: learning rate
        alpha: exponential decay factor
    '''

    eta: float
    alpha: float

    def __init__(self, *, alpha: float = 0.9, eta: float = 0.1):
        '''Initalizes `eta` and `aplha` fields'''
        raise NotImplementedError()

    def optimize(self, oracle: Oracle, x0: np.ndarray, *,
                 max_iter: int = 100, eps: float = 1e-5) -> np.ndarray:
        '''Optimizes a function specified as `oracle` starting from point `x0`.
        The optimizations stops when `max_iter` iterations were completed or 
        the L2-norm of the current gradient is less than `eps`

        Args:
            oracle: function to optimize
            x0: point to start from
            max_iter: maximal number of iterations
            eps: threshold for L2-norm of gradient

        Returns:
            A point at which the optimization stopped
        '''
        raise NotImplementedError()

• alpha — скорость затухания момента,
• eta — learning rate.

• oracle — оптимизируемая функция,
• x0 — начальная точка,
• max_iter — максимальное количество итераций,
• eps — пороговое значение L2 нормы градиента.

Класс Oracle описывает оптимизируемую функцию

import numpy as np

class Oracle:
    '''Provides an interface for evaluating a function and its derivative at arbitrary point'''
    
    def value(self, x: np.ndarray) -> float:
        '''Evaluates the underlying function at point `x`

        Args:
            x: a point to evaluate funciton at

        Returns:
            Function value
        '''
        raise NotImplementedError()
        
    def gradient(self, x: np.ndarray) -> np.ndarray:
        '''Evaluates the underlying function derivative at point `x`

        Args:
            x: a point to evaluate derivative at

        Returns:
            Function derivative
        '''
        raise NotImplementedError()

Формат выходных данных

Код решения должен содержать только определение и реализацию класса.

Задача D. AdaGrad ≡

Условие

Требуется реализовать на языке Python класс AdaGrad, который описывает алгоритм адаптивного градиентного спуска и имеет следующий интерфейс

import numpy as np

class AdaGrad:
    '''Represents an AdaGrad optimizer

    Fields:
        eta: learning rate
        epsilon: smoothing term
    '''

    eta: float
    epsilon: float

    def __init__(self, *, eta: float = 0.1, epsilon: float = 1e-8):
        '''Initalizes `eta` and `epsilon` fields'''
        raise NotImplementedError()

    def optimize(self, oracle: Oracle, x0: np.ndarray, *,
                 max_iter: int = 100, eps: float = 1e-5) -> np.ndarray:
        '''Optimizes a function specified as `oracle` starting from point `x0`.
        The optimizations stops when `max_iter` iterations were completed or 
        the L2-norm of the gradient at current point is less than `eps`

        Args:
            oracle: function to optimize
            x0: point to start from
            max_iter: maximal number of iterations
            eps: threshold for L2-norm of gradient

        Returns:
            A point at which the optimization stopped
        '''
        raise NotImplementedError()

• eta — learning rate,
• epsilon — сглаживающий коэффициент.

• oracle — оптимизируемая функция,
• x0 — начальная точка,
• max_iter — максимальное количество итераций,
• eps — пороговое значение L2 нормы градиента.

Класс Oracle описывает оптимизируемую функцию

import numpy as np

class Oracle:
    '''Provides an interface for evaluating a function and its derivative at arbitrary point'''
    
    def value(self, x: np.ndarray) -> float:
        '''Evaluates the underlying function at point `x`

        Args:
            x: a point to evaluate funciton at

        Returns:
            Function value
        '''
        raise NotImplementedError()
        
    def gradient(self, x: np.ndarray) -> np.ndarray:
        '''Evaluates the underlying function derivative at point `x`

        Args:
            x: a point to evaluate derivative at

        Returns:
            Function derivative
        '''
        raise NotImplementedError()

Формат выходных данных

Код решения должен содержать только определение и реализацию класса.

Задача E. RMSProp ≡

Условие

Требуется реализовать на языке Python класс RMSProp, который описывает одноименный алгоритм и имеет следующий интерфейс

import numpy as np

class RMSProp:
    '''Represents an RMSProp optimizer

    Fields:
        eta: learning rate
        gamma: exponential decay factor
        epsilon: smoothing term
    '''

    eta: float
    gamma: float
    epsilon: float

    def __init__(self, *, eta: float = 0.1, gamma: float = 0.9, epsilon: float = 1e-8):
        '''Initalizes `eta`, `gamma` and `epsilon` fields'''
        raise NotImplementedError()

    def optimize(self, oracle: Oracle, x0: np.ndarray, *,
                 max_iter: int = 100, eps: float = 1e-5) -> np.ndarray:
        '''Optimizes a function specified as `oracle` starting from point `x0`.
        The optimizations stops when `max_iter` iterations were completed or 
        the L2-norm of the gradient at current point is less than `eps`

        Args:
            oracle: function to optimize
            x0: point to start from
            max_iter: maximal number of iterations
            eps: threshold for L2-norm of gradient

        Returns:
            A point at which the optimization stopped
        '''
        raise NotImplementedError()

• eta — learning rate,
• gamma — коэффициент затухания,
• epsilon — сглаживающий коэффициент.

• oracle — оптимизируемая функция,
• x0 — начальная точка,
• max_iter — максимальное количество итераций,
• eps — пороговое значение L2 нормы градиента.

Класс Oracle описывает оптимизируемую функцию

import numpy as np

class Oracle:
    '''Provides an interface for evaluating a function and its derivative at arbitrary point'''
    
    def value(self, x: np.ndarray) -> float:
        '''Evaluates the underlying function at point `x`

        Args:
            x: a point to evaluate funciton at

        Returns:
            Function value
        '''
        raise NotImplementedError()
        
    def gradient(self, x: np.ndarray) -> np.ndarray:
        '''Evaluates the underlying function derivative at point `x`

        Args:
            x: a point to evaluate derivative at

        Returns:
            Function derivative
        '''
        raise NotImplementedError()

Формат выходных данных

Код решения должен содержать только определение и реализацию класса.

Задача F. Adam ≡

Условие

Требуется реализовать на языке Python класс Adam, который описывает одноименный алгоритм и имеет следующий интерфейс

import numpy as np

class Adam:
    '''Represents an Adam optimizer

    Fields:
        eta: learning rate
        beta1: first moment decay rate
        beta2: second moment decay rate
        epsilon: smoothing term
    '''

    eta: float
    beta1: float
    beta2: float
    epsilon: float

    def __init__(self, *, eta: float = 0.1, beta1: float = 0.9, beta2: float = 0.999, epsilon: float = 1e-8):
        '''Initalizes `eta`, `beta1` and `beta2` fields'''
        raise NotImplementedError()

    def optimize(self, oracle: Oracle, x0: np.ndarray, *,
                 max_iter: int = 100, eps: float = 1e-5) -> np.ndarray:
        '''Optimizes a function specified as `oracle` starting from point `x0`.
        The optimizations stops when `max_iter` iterations were completed or 
        the L2-norm of the gradient at current point is less than `eps`

        Args:
            oracle: function to optimize
            x0: point to start from
            max_iter: maximal number of iterations
            eps: threshold for L2-norm of gradient

        Returns:
            A point at which the optimization stopped
        '''
        raise NotImplementedError()

• eta — learning rate,
• beta1 — коэффициент затухания первого момента,
• beta2 — коэффициент затухания второго момента,
• epsilon — сглаживающий коэффициент.

• oracle — оптимизируемая функция,
• x0 — начальная точка,
• max_iter — максимальное количество итераций,
• eps — пороговое значение L2 нормы градиента.

Класс Oracle описывает оптимизируемую функцию

import numpy as np

class Oracle:
    '''Provides an interface for evaluating a function and its derivative at arbitrary point'''
    
    def value(self, x: np.ndarray) -> float:
        '''Evaluates the underlying function at point `x`

        Args:
            x: a point to evaluate funciton at

        Returns:
            Function value
        '''
        raise NotImplementedError()
        
    def gradient(self, x: np.ndarray) -> np.ndarray:
        '''Evaluates the underlying function derivative at point `x`

        Args:
            x: a point to evaluate derivative at

        Returns:
            Function derivative
        '''
        raise NotImplementedError()

Формат выходных данных

Код решения должен содержать только определение и реализацию класса.

Задача G. Линейная регрессия. Основы ≡

Условие

Требуется реализовать следующие функции на языке Python.

def linear_func(theta, x)                  # function value
def linear_func_all(theta, X)              # 1-d np.array of function values of all rows of the matrix X
def mean_squared_error(theta, X, y)        # MSE value of current regression
def grad_mean_squared_error(theta, X, y)   # 1-d array of gradient by theta

theta — одномерный np.array

x — одномерный np.array

X — двумерный np.array. Каждая строка соответствует по размерности вектору theta

y — реальные значения предсказываемой величины

Матрица X имеет размер M × N. M строк и N столбцов.

Используется линейная функция вида: h_θ(x) = θ₁ x₁ + θ₂ x₂ + ...  + θ_n x_N

Mean squared error (MSE) как функция от θ: J(θ) = 1MM∑i = 1(y_i − h_θ(x⁽ⁱ⁾))². Где x⁽ⁱ⁾ — i-я строка матрицы X

Градиент функции MSE: ∇ J(θ) = { ∂ J∂ θ₁, ∂ J∂ θ₂, ..., ∂ J∂ θ_N}

Пример

X = np.array([[1,2],[3,4],[4,5]])

theta = np.array([5, 6])

y = np.array([1, 2, 1])

linear_func_all(theta, X) # --> array([17, 39, 50])

mean_squared_error(theta, X, y) # --> 1342.0

grad_mean_squared_error(theta, X, y) # --> array([215.33333333, 283.33333333])

Формат выходных данных

Код должен содержать только реализацию функций.

Задача H. Найти линейную регрессию ≡

Условие

Требуется реализовать функцию на языке Python, которая находит линейную регрессию заданных векторов, используя метрику MSE.

def fit_linear_regression(X, y)   # np.array of linear regression coefs

X — двумерный np.array. Каждая строка соответствует отдельному примеру.

y — реальные значения предсказываемой величины

Формат выходных данных

Код должен содержать только реализацию функций.

Задача I. Entropy ≡

Условие

Требуется реализовать на языке Python функцию, вычисляющую значение энтропии заданной выборки.

entropy(y) =  − ∑v = set(y)p(v)log p(v)

где set(y) — множество уникальных значений вектора y.

import numpy as np

def entropy(y: np.ndarray) -> float:
    """Computes entropy value for labels `y`.
    
    Arguments:
        y: 1d array of integers, sample labels
        
    Returns:
        float, entropy value for labels `y`"""
    pass

Функция принимает единственный параметр y — одномерный np.array, значения классов в обучающей выборке.

При решении задачи следует использовать натуральный логарифм.

Формат выходных данных

Код должен содержать только реализацию функции. Запрещено пользоваться любыми готовыми реализациями вычисления функции entropy.

Задача J. Gini ≡

Условие

Требуется реализовать на языке Python функцию, вычисляющую значение gini impurity заданной выборки.

gini(y) = 1 − ∑v = set(y)p²(v)

где set(y) — множество уникальных значений вектора y.

import numpy as np

def gini(y: np.ndarray) -> float:
    """Computes gini impurity value for labels `y`.
    
    Arguments:
        y: 1d array of integers, sample labels
        
    Returns:
        float, gini impurity value for labels `y`"""
    pass

y — одномерный np.array — значения классов в выборке

Формат выходных данных

Код должен содержать только реализацию функции. Запрещено пользоваться любыми готовыми реализациями вычисления функции gini.

Примеры тестов

3 2 4 4 2 0 1 3 0 1

0.8

Задача K. Decision tree split ≡

Условие

Требуется реализовать следующие функцию на языке Python.

def tree_split(X, y, criterion)   # col, row of best split

X — двумерный np.array — обучающая выборка

y — одномерный np.array — значения классов в обучающей выборке

criterion — строковое значение — вид критерия 'var', 'gini' или 'entropy'

tree_split должен возвращать номер признака и номер значения из обучающей выборки, которое будет использоваться в качестве порогового

Таким образом, tree_split возвращает наилучшее бинарное разделение по правилу вида x^col ≤ X[row, col]

Формат выходных данных

Код должен содержать только реализацию функции.

Задача L. Lasso ≡

Условие

Пусть имеется задача регрессии f(x) = a ⋅ x + b ≈ y. Требуется найти коэффициенты регрессии a, такие, что |{a_i | a_i ∈ a, a_i = 0}| = k,  0 < k ⩽ |a| = m. При этом должно выполняться условие R² = 1 − n∑i = 1(y_i − f(X_i))²n∑i = 1(y_i − y)² ⩾ s. При решении задачи предполагается использование алгоритма Lasso.

Формат входных данных

Данные для обучения содержатся в файле. Качество модели будет рассчитано на скрытом наборе данных

Первая строка входных данных содержит натуральное число N — количество тестов. В следующих N блоках содержится описание тестов. Первая строка блока содержит целые числа n — количество примеров обучающей выборки, m — размерность пространства, k — необходимое количество нулевых коэффициентов, и вещественное число s — минимальное значение метрики R². Следующие n строк содержат по m + 1 вещественному числу — координаты точки пространства и значение целевой переменной y.

Формат выходных данных

Решение должно представлять собой текстовый файл содержащий N строк — коэффициенты a и b линейной регрессии разделённые символом пробел.

Примеры тестов

1
10 5 1 0.8
-0.5  -0.26 -0.11 -0.66  0.49 -24.89
 0.08 -0.38  0.6   1.29  0.42  62.2
 0.82  0.12  0.54  1.33 -0.82  47.55
-0.36  0.54 -0.6   0.55 -0.01 -15.96
-0.91 -0.71  0.59  1.0   0.43 -11.11
-0.97 -0.78  0.2  -0.93  1.24 -17.04
 0.29  0.77 -0.87 -0.05 -0.71 -38.97
 0.19 -0.16  1.0   0.63  1.79 188.63
 0.22 -2.38  3.0   0.22 -0.53  23.32
 0.36 -0.84  1.05 -1.06 -0.06  15.31

43.69 0.0 10.48 16.86 46.25 6.39

Задача M. k-point crossover ≡

Условие

Требуется на языке Python реализовать методы точечного кроссовера.

Функция single_point_crossover(a, b, point) выполняет одноточечный кроссовер, значения справа от точки кроссовера меняются местами.

Функция two_point_crossover(a, b, first, second) выполняет двухточечный кроссовер, значения между точек кроссовера меняются местами.

Функция k_point_crossover(a, b, points) выполняет k-точечный кроссовер, значения между каждой чётной парой точек меняются местами.

Функции должны иметь следующий интерфейс

import numpy as np

def single_point_crossover(a: np.ndarray, b: np.ndarray, point: int) -> tuple[np.ndarray, np.ndarray]:
    """Performs single point crossover of `a` and `b` using `point` as crossover point.
    Chromosomes to the right of the `point` are swapped

    Args:
        a: one-dimensional array, first parent
        b: one-dimensional array, second parent
        point: crossover point

    Return:
        Two np.ndarray objects -- the offspring"""

    raise NotImplemetnedError()


def two_point_crossover(a: np.ndarray, b: np.ndarray, first: int, second: int) -> tuple[np.ndarray, np.ndarray]:
    """Performs two point crossover of `a` and `b` using `first` and `second` as crossover points.
    Chromosomes between `first` and `second` are swapped

    Args:
        a: one-dimensional array, first parent
        b: one-dimensional array, second parent
        first: first crossover point
        second: second crossover point

    Return:
        Two np.ndarray objects -- the offspring"""

    raise NotImplemetnedError()


def k_point_crossover(a: np.ndarray, b: np.ndarray, points: np.ndarray) -> tuple[np.ndarray, np.ndarray]:
    """Performs k point crossover of `a` and `b` using `points` as crossover points.
    Chromosomes between each even pair of points are swapped

    Args:
        a: one-dimensional array, first parent
        b: one-dimensional array, second parent
        points: one-dimensional array, crossover points

    Return:
        Two np.ndarray objects -- the offspring"""

    raise NotImplemetnedError()

Формат выходных данных

Код решения должен содержать импортируемые модули, определение и реализацию функций.

Примеры тестов

0 1 2 3 4 4 3 2 1 0
9 8 7 6 5 5 6 7 8 9

0 1 2 6 5 4 3 7 8 9
9 8 7 3 4 5 6 2 1 0

0 1 7 6 5 5 6 7 8 0
9 8 2 3 4 4 3 2 1 9
            

Задача N. Stochastic universal sampling ≡

Условие

Требуется на языке Python реализовать алгоритм Stochastic universal sampling.

Функция должна иметь следующий интерфейс

import numpy as np

def sus(fitness: np.ndarray, n: int, start: float) -> list:
    """Selects exactly `n` indices of `fitness` using Stochastic universal sampling alpgorithm. 

    Args:
        fitness: one-dimensional array, fitness values of the population, sorted in descending order
        n: number of individuals to keep
        start: minimal cumulative fitness value

    Return:
        Indices of the new population"""

    raise NotImplementedError()

Параметрами функции являются:

• fitness — одномерный массив значений функции приспособленности, отсортированный по убыванию,
• n — количество особей, которых нужно оставить,
• start — минимальное кумулятивное значение функции приспособленности.

Функция возвращает список индексов выбранных особей

Формат выходных данных

Код решения должен содержать импортируемые модули, определение и реализацию функции.

Примеры тестов

10 4 1
            

Задача O. Метод ближайших соседей. Основы ≡

Условие

Требуется реализовать следующие функцию на языке Python.

def knn_predict_simple(X, y, x, k)     # array of pairs -- class and number of votes of neighbors

X — двумерный np.array — обучающая выборка

y — реальные значения классов в обучающей выборке

x — одномерный np.array-- тестовый пример

k — количество соседей, которые нужно рассматривать

Функция возвращает массив пар (класс, количество голосов) только для классов которые встречаются среди k ближайших соседей!

Для поиска ближайшего примера использовать евклидово расстояние.

Формат выходных данных

Код должен содержать только реализацию функции.

Задача P. Leave-one-out (метод скользящего контроля) ≡

Условие

Требуется реализовать функцию leave-one-out score на языке Python. Результат функции должен быть целочисленным, то есть его НЕ следует нормировать на размер выборки.

def loo_score(predict, X, y, k)     # integer loo score for predict function

predict — функция predict(X, y, x, k) , обучающая некоторый алгоритм на выборке X, y с параметром k и дающая предсказание на примере x

X — двумерный np.array — обучающая выборка

y — реальные значения классов в обучающей выборке

k — количество соседей, которые нужно рассматривать

Формат выходных данных

Код должен содержать только реализацию функции.

Задача Q. Border ratio ≡

Условие

Пусть на некотором наборе точек X = {x_i}ni = 1, x_i ∈ R^m задана функция f: R^m↦N. Требуется написать программу, вычисляющую значение border ratio α(x) = ∥x̂ − y∥₂∥ x − y∥₂, ∀ x ∈ X, где y = arg miny ∈ X, f(x) ≠ f(y)∥ x − y∥₂, x̂ = arg minx̂ ∈ X, f(x) = f(x̂)∥x̂ − y∥₂.

Формат входных данных

Первая строка входного файла содержит натуральные числа n, m — количество точек и размерность пространства соответственно. В следующих n строках содержится m вещественных чисел и одно натуральное число — координаты точки и значение функции в этой точке.

Формат выходных данных

Выходной файл должен содержать n вещественных чисел — значения border ratio каждой точки с точностью не менее трёх знаков после запятой.

Ограничения

6 ⩽ n ⩽ 1500

2 ⩽ m ⩽ 50

Примеры тестов

6 2
0 0 0
0 2 1
1 2 0
4 2 1
3 0 1
4 0 0

0.5 1.0 1.0 0.5 1.0 1.0

10 2
0 0 0
0 2 0
4 2 0
6 2 0
4 4 1
6 1 1
6 6 1
0 5 2
0 6 2
0 7 2

0.6 1.0 1.0 1.0 1.0 1.0 0.25 1.0 0.75 0.6

Задача R. KMeans ≡

Условие

Пусть задан некоторый набор точек X = {x_i}ni = 1, x_i ∈ R^m. Требуется выполнить кластеризацию точек на k кластеров, используя наивный алгоритм KMeans.

Формат входных данных

Первая строка входных данных содержит натуральные числа n, m, k, t — количество точек, размерность пространства, количество кластеров и максимальное количество итераций соответственно. В каждой из следующих n строк содержится m вещественных чисел и одно натуральное число — координаты точки и начальное значение кластера точки. Значения кластеров нумеруются от 0 до k − 1.

Формат выходных данных

Выходной данные должны содержать n натуральных чисел — номер кластера каждой точки.

Ограничения

6 ⩽ n ⩽ 1000

2 ⩽ m, k ⩽ 10

10 ⩽ t ⩽ 10⁹

Примеры тестов

6 2 2 10
0 0 0
0 3 1
3 0 1
2 5 0
5 2 0
5 5 1

0
0
0
1
1
1