Problem A. Area 51 ≡

Author:NEERC 2005
Input file: area.in   Time limit:2 sec
Output file: area.out   Memory limit:256 Mb

Statement

Michael and Nick are living near the famous top-secret Area 51 facility. The facility is enclosed by a fence and is so large that for the purpose of this problem we consider the fence being a line that stretches infinitely into both directions.

Only extremely brave boys are not scared to go to the fence and peek at the facility. Nick is among the brave ones. He once came to the fence and saw a number of chimneys with distinct shapes. As a proof of his bravery he tells everybody what chimneys he saw from his left to his right.

Michael’s father is working at Area51”and has a facility’s map at his home. Michael found this map and he can now verify Nick's claim of being near the facility's fence. However, it turns out to be complicated, and your task is to write a program to perform this verification.

On a map distinctly shaped chimneys are denoted by capital letters from A to Z. Each letter denotes a distinct shape, but chimneys with this shape can appear more than once on a map. The map uses Cartesian coordinate system oriented so that the fence is Ox axis and all chimneys are located on a half-plane with a positive y coordinate. All chimneys are considered to be points (their sizes and actual geometrical shapes are ignored for the purpose of this problem).

Nick claims that he looked from a point on the fence where no two chimneys were on the same line of his sight (a line that originates from his point of view). It means that at the point he looked from, all the chimneys he saw had a well-defined order from left to right.

Michael have already made a preliminary verification of Nick's claim. He made sure that the number of distinctly shaped chimneys matches their number on the map. Now Michael needs to perform a final verification to get a list of x coordinates on a fence (if any) where the corresponding arrangement of chimneys could be seen from. This information shall be presented as an ordered list of open intervals (a1, b1), (a2, b2), …, (an, bn), so that a1 < b1 ≤ a2 < b2 ≤ … ≤ an < bn. Asterisk symbol ("*") is used in place of a1 and/or bn to denote interval that extends to infinity on the left or on the right correspondingly. Note, that bi = ai+1 = x in case where Nick could not have been at the point x on a fence, because he would have seen more than one chimney on a single line of his sight, but being to the left or to the right of x yields the order of chimneys that he saw.

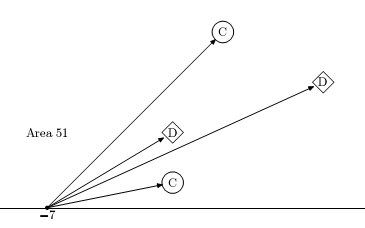
The picture below shows that if the boy looks from the point x = −7 he sees the chimneys in the following order: C, D, D, C. It is so for any point from the set (−∞,−11) ∪ (−11,−3.5) ∪ (14,+∞) — the first example from the problem statement.

Input file format

The first line of the input file contains an integer number m the number of chimneys at the "Area 51" facility. The second line of the input file contains a string of m letters from A to Z that describe the chimneys that Nick saw from his left to his right. A single letter can be used more than once (if Nick saw the same shape more than once). Then follow m lines that describe chimneys on the map. Each line contains three tokens separated by spaces — chimney shape letter (from A to Z), and two integers xi and yi — chimney coordinates. On these m lines letters appear in arbitrary order, but each letter from A to Z appears the same number of times as on the second line of the input file. No two chimneys have the same coordinates.

Output file format

Write to the first line of the output file a single integer number n — the number of intervals that describe x coordinates on a fence where Nick could have seen the corresponding arrangement of chimneys from. Write to the second line of the output file 2 n numbers a1, b1, …, an, bn using "*" instead of a number a1 and/or bn to denote infinity. Numbers must be precise up to 10−6.

Constraints

1 ≤ m ≤ 100, −100 ≤ xi ≤ 100, 0 < yi ≤ 100

Sample tests

No. Input file (area.in) Output file (area.out)
1 
4
CDDC
C 0 7
D 4 5
C -2 1
D -2 3
 
3
* -11 -11 -3.5 14 *
2 
4
DCCD
C 0 7
D 4 5
C -2 1
D -2 3
 
2
-3.5 -2.333333 -2.333333 -2
3 
4
DCDC
C 0 7
D 4 5
C -2 1
D -2 3
 
0

Problem B. Beach cut ≡

Author:B. Vasilyev, A. Klenin
Input file: input.txt   Time limit:4 sec
Output file: output.txt   Memory limit:200 Mb

Statement

The seashore is represented by a polyline without self-intersections, described by a sequence of vertices (x1, y1), … (xN, yN). It also has a property that xi < xi + 1. The sea is above the line, and the beach — below.

Your program must connect two vertices with a straight line not longer than L chosen so as to maximize the beach area enclosed between that line and the shore. The line must not intersect with the sea and may only touch, not intersect, the shore polyline.

Input file format

Input file contains integer numbers N L, followed by N pairs of integers x1 y1… xN yN.

Output file format

Output file must contain a single floating point value — the maximum area that can be cut (it may be zero). The area must be output exactly, i.e. without any rounding at all.

Constraints

3 ≤ N ≤ 5000, 0 ≤ xi, yi, L ≤ 1000000

Sample tests

No. Input file (input.txt) Output file (output.txt)
1 
5 4
0 0  1 3  2 0  3 3  4 0
 
6
2 
3 10
100 100  101 0  102 100
 
0

Problem C. Smooth convex hull ≡

Author:T. Chistyakov, A. Klenin
Input file: input.txt   Time limit:3 sec
Output file: output.txt   Memory limit:64 Mb

Statement

There are N points on a plane. Convex hull is such a convex polygon with the least possible area, that all the given points are either within its interior or belong to its border.

Let's say that one convex polygon is smoother that the other one if it's sharpest angle is more obtuse than the sharpest angle of the other one.

Your task is to make the convex hull of the given set of points as smooth as possible. To do it you are allowed to exclude no more than one point from the given set.

Input file format

Input file contains integer N, then N pairs of real numbers xi yi describing given points. There are no duplicate points in the input file.

Output file format

Output file must contain a single number: the sharpest angle (in radians) in the most smooth convex hull with absolute error less than 0.01.

Constraints

3 ≤ N ≤ 1000

1 ≤ xi, yi ≤ 106

Sample tests

No. Input file (input.txt) Output file (output.txt)
1 
5
1 1  2 10  1 3  3 1  3 3 

1.57
2 
4
1 1  1 3  3 1  3 3 

1.57

Problem D. Min perimeter ≡

Author:Google Code Jam, World Finals 2009
Input file: input.txt   Time limit:10 sec
Output file: output.txt   Memory limit:256 Mb

Statement

You will be given a set of points with integer coordinates. You are asked to compute the smallest perimeter of a triangle with distinct vertexes from this set of points.

Input file format

The first line contains one integer N  — number of points.

Each of the next N lines contains two integer numbers xi, yi  — coordinates of i-th point.

Output file format

Output file should contain one real number  — the minimum perimeter. Answers with a relative or absolute error of at most 10−7 will be considered correct. Degenerate triangles -— triangles with zero area -— are ok.

Constraints

0 ≤ n ≤ 106

0 ≤ xi, yi ≤ 109

0.044s 0.004s 17