Задача A. Космическое поселение
Условие
Для освоения Марса требуется построить исследовательскую базу.
База должна состоять из N одинаковых модулей.
Каждый модуль представляет собой жилой отсек, который в основании имеет форму
прямоугольника размером A × B метров.
Для повышения надежности модулей инженеры могут добавить вокруг каждого модуля
дополнительный защитный слой.
Толщина этого слоя должна составлять целое число метров,
и все модули должны иметь одинаковую толщину защитного слоя.
Модуль с защитным слоем, толщина которой равна D метрам,
будет иметь в основании форму прямоугольника размером (A + 2 D) × (B + 2 D) метров.
Все модули должны быть расположены на заранее подготовленном прямоугольном поле размером W × H метров.
При этом они должны быть организованы в виде регулярной сетки,
их стороны должны быть параллельны сторонам поля, и модули должны быть ориентированы одинаково.
Требуется написать программу, которая по заданным количеству и размеру модулей,
а также размеру поля для их размещения, определяет максимальную
толщину дополнительного защитного слоя, который можно добавить к каждому модулю.
Пояснения к примеру
В первом примере можно установить дополнительный защитный слой толщиной 2 метра
и разместить модули на поле, как показано на рисунке.
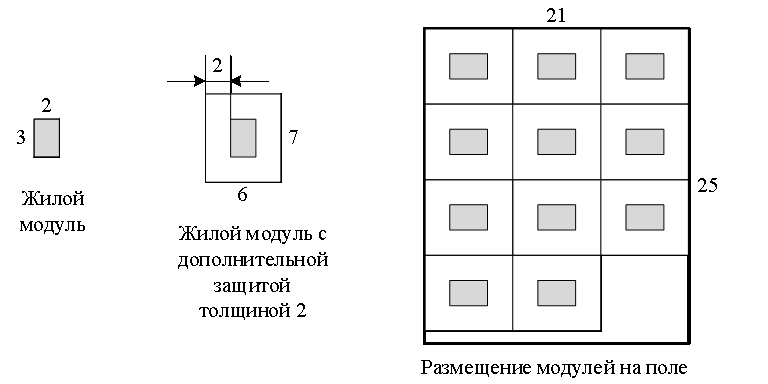
Во втором примере жилой отсек имеет в основании размер 5 × 5 метров, а поле — размер 6 × 6 метров.
Добавить дополнительный защитный слой к модулю нельзя.
Формат входного файла
Входной файл содержит пять разделенных пробелами целых чисел: N, A, B, W, H.
Гарантируется, что без дополнительного защитного слоя все модули можно разместить в поселении описанным образом.
Формат выходного файла
Выходной файл должен содержать одно целое число: максимальную возможную толщину дополнительного защитного слоя.
Если дополнительный защитный слой установить не удастся, требуется вывести число 0.
Ограничения
1 ≤ N, A, B, W, H ≤ 1018
Система оценки и описание подзадач
Подзадача 1 (26 баллов)
1 ≤ N ≤ 1000; 1 ≤ A, B, W, H ≤ 1000.
Баллы за подзадачу начисляются только в случае, если все тесты успешно пройдены.
Подзадача 2 (23 балла)
1 ≤ N ≤ 1000; 1 ≤ A, B, W, H ≤ 109.
Баллы за подзадачу начисляются только в случае, если все тесты успешно пройдены.
Подзадача 3 (24 балла)
1 ≤ N ≤ 109; 1 ≤ A, B, W, H ≤ 1018.
В этой подзадаче 8 тестов, каждый тест оценивается в 3 балла. Баллы за каждый тест начисляются независимо.
Подзадача 4 (27 баллов)
1 ≤ N ≤ 1018; 1 ≤ A, B, W, H ≤ 1018.
В этой подзадаче 9 тестов, каждый тест оценивается в 3 балла. Баллы за каждый тест начисляются независимо.
Получение информации о результатах окончательной проверки
По запросу сообщается результат окончательной проверки на каждом тесте.
Примеры тестов
| № |
Входной файл (space.in) |
Выходной файл (space.out) |
|---|
| 1 |
11 2 3 21 25
|
2
|
| 2 |
1 5 5 6 6
|
0
|
Problem B. Lin-log sort 2
Statement
You are to write a program that receives a sequence of integer numbers and sorts it,
i. e. writes out all elements in ascending order.
Input file format
Input file contains integer
N — length of the sequnece,
followed by
N integer numbers — elements of the sequence.
Output file format
Output file must contain
N integer numbers,
which must be elements of the source sequence printed in ascending order.
Constraints
0 ≤ N ≤ 100000.
Sequence elements are less than 10
9 by absolute value.
Sample tests
| No. |
Input file (input.txt) |
Output file (output.txt) |
|---|
| 1 |
5 4 3 10 3 1
|
1 3 3 4 10
|
Problem C. Heapsort
Statement
A well known algorithm called heapsort is a
deterministic sorting algorithm taking O(n log n) time
and O(1) additional memory. Let us describe ascending sorting
of an array of different integer numbers.
The algorithm consists of two phases. In the first phase,
called heapification, the array of integers to be sorted
is converted to a heap. An array a[1…n] of integers
is called a heap if for all 1 ≤ i ≤ n the following heap conditions
are satisfied:
- if 2i ≤ n
then a[i] > a[2i];
- if 2i + 1 ≤ n then a[i] > a[2i + 1].
We can interpret an array as a binary tree, considering children
of element a[i] to be a[2i] and a[2i + 1]. In this case
the parent of a[i] is a[i div 2], where i div 2 = floor(i / 2).
In terms of trees
the property of being a heap means that for each node its value is greater
than the values of its children.
In the second phase the heap is turned into a sorted array.
Because of the heap condition the greatest element
in the heapified array is a[1]. Let us exchange it with a[n],
now the greatest element of the array is at its correct position
in the sorted array. This is called extract-max.
Now let us consider the part of the array a[1 ... n-1]. It may be
not a heap because the heap condition may fail for i=1.
If it is so (that is, either a[2] or a[3], or both are greater
than a[1]) let us exchange the greatest child of a[1] with it, restoring
the heap condition for i=1. Now it is possible that the heap condition
fails for the position that now contains the former value of a[1]. Apply the same
procedure to it, exchanging it with its greatest child. Proceeding so
we convert the whole array a[1 ... n-1] to a heap.
This procedure is called sifting down.
After converting the part a[1 ... n-1] to a heap by sifting, we
apply extract-max again, putting second greatest element of
the array to a[n-1], and so on.
For example, let us see how the heap a=(5, 4, 2, 1, 3) is converted to
a sorted array. Let us make the first extract-max. After that the array
turns to (3, 4, 2, 1, 5). Heap condition fails
for a[1] = 3 because its child a[2] = 4 is greater than it.
Let us sift it down, exchanging a[1] and a[2]. Now the array is
(4, 3, 2, 1, 5). The heap condition is satisfied
for all elements, so sifting is over. Let us make extract-max again.
Now the array turns to (1, 3, 2, 4, 5). Again
the heap condition fails for a[1]; exchanging it with its greatest
child we get the array (3, 1, 2, 4, 5) which is
the correct heap. So we make extract-max and get
(2, 1, 3, 4, 5). This time the heap condition
is satisfied for all elements, so we make extract-max, getting
(1, 2, 3, 4, 5). The leading
part of the array is a heap, and the last
extract-max finally gives (1, 2, 3, 4, 5).
It is known that heapification can be done in O(n) time. Therefore,
the most time consuming operation in heapsort algorithm is sifting,
which takes O(n * log (n)) time.
In this problem you have to find a heapified array containing
different numbers from 1 to n, such that when
converting it to a sorted array, the total number of exchanges in
all sifting operations is maximal possible. In the example above the
number of exchanges is 1+1+0+0+0 = 2, which is not the maximum.
(5, 4, 3, 2, 1) gives the maximal number of 4 exchanges for n=5.
Input file format
Input file contains
n.
Output file format
Output the array containing
n different integer
numbers from 1 to
n, such that it is a heap,
and when converting it to a sorted array,
the total number of exchanges in sifting operations is
maximal possible. Separate numbers by spaces.
Constraints
1 ≤ n ≤ 50000
Sample tests
| No. |
Input file (heapsort.in) |
Output file (heapsort.out) |
|---|
| 1 |
6
|
6 5 3 2 4 1
|
Задача D. Зельеварение
Условие
Юный волшебник Вася на уроках зельеварения недавно изобрел новый вид зелий.
Пары разработанного им зелья увеличивают или уменьшает температуру окружающей
среды на заданное Васей при варке зелья количество градусов.
Вася сварил N таких зелий, i-е зелье увеличивает температуру окружающей среды на целое число ai градусов.
Каждое зелье он налил в отдельную колбу, чтобы зелья начали испаряться.
Все колбы одинаковы. Эффекты от паров зелий в разных колбах складываются.
Колбы Вася выставил в ряд и начал наблюдать за изменением температуры в комнате.
К сожалению, температура в комнате очень быстро стала некомфортной.
И тут Вася подумал, почему бы не сделать температуру воздуха в комнате равной T0 + K,
где T0 — температура в комнате до приготовления зелий.
Он тут же вспомнил, что на уроках заклинаний он недавно научился заклинанию исчезновения!
Заклинание позволяет ему безвозвратно уничтожить любой непрерывный отрезок подряд идущих колб
вместе с их влиянием на температуру воздуха в комнате.
Используя только это заклинание, Вася хочет сделать температуру в комнате желаемой.
Вася, в виду его юности, еще слишком слаб, чтобы читать сколько угодно заклинаний, когда ему вздумается.
Он может прочитать максимум два таких заклинания.
Кроме того, Вася хочет уничтожить как можно больше колб, чтобы потом тратить меньше сил на их отмывание.
Помогите Васе определить, на какие колбы направить свои заклинания.
Формат входного файла
Первая строка входного файла содержит два целых числа N K —– количество колб с зельями и температура,
на которую Вася хочет изменить исходную в комнате.
Вторая строка содержит N целых чисел, i-е число — количество градусов,
на которое увеличится температура окружающей среды из-за паров i-ой колбы.
Формат выходного файла
В выходной файл выведите единственное число — максимальное количество уничтоженных колб или −1,
если требуемой температуры нельзя достигнуть.
Ограничения
1 ≤ N ≤ 2 ⋅ 103
−107 ≤ K ≤ 107
−104 ≤ ai ≤ 104
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
1 0
1
|
1
|
| 2 |
5 1
1 2 3 -1 -1
|
4
|
