Задача A. Разрезанная рамка
Условие
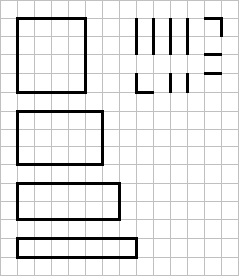
Прямоугольная рамка была разрезана на N кусков.
Каждый кусок может представлять собой либо отрезок прямой, либо "уголок" — два отрезка,
соединённых под прямым углом.
По данным длинам отрезков требуется восстановить исходную рамку или определить,
что это невозможно.
Куски можно поворачивать, но нельзя отражать. Требуется использовать все куски.
Формат входного файла
Входной файл содержит число кусков
N, за которым следуют
N пар целых чисел
ai bi,
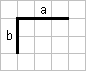
описывающих длину двух отрезков "уголка"
i-го куска.
Если кусок является отрезком, то
ai = 0 либо
bi = 0.
Формат выходного файла
Выходной файл должен содержать два положительных целых числа
W H —
ширину и высоту рамки, при этом
W ≥ H.
Если решения не существует, следует выдать число
−1.
Если решений несколько, следует выдать решение с максимальным значением
W.
Ограничения
1 ≤ N ≤ 10,
0 ≤ ai, bi ≤ 100
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
10
1 1 1 1
1 0 1 0 1 0 1 0
0 2 0 2 0 2 0 2
|
7 1
|
| 2 |
5
1 1 1 1 1 1 1 1 5 0
|
-1
|
Problem B. Beach cut
Statement
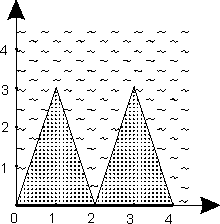
The seashore is represented by a polyline without self-intersections, described by
a sequence of vertices (x1, y1), … (xN, yN).
It also has a property that xi < xi + 1.
The sea is above the line, and the beach — below.
Your program must connect two vertices with a straight line not longer than L
chosen so as to maximize the beach area enclosed between that line and the shore.
The line must not intersect with the sea and may only touch, not intersect,
the shore polyline.
Input file format
Input file contains integer numbers
N L,
followed by
N pairs of integers
x1 y1… xN yN.
Output file format
Output file must contain a single floating point value — the maximum area that can be cut (it may be zero).
The area must be output
exactly, i.e. without any rounding at all.
Constraints
3 ≤ N ≤ 5000,
0 ≤ xi, yi, L ≤ 1000000
Sample tests
| No. |
Input file (input.txt) |
Output file (output.txt) |
|---|
| 1 |
5 4
0 0 1 3 2 0 3 3 4 0
|
6
|
| 2 |
3 10
100 100 101 0 102 100
|
0
|
Problem C. Min perimeter
Statement
You will be given a set of points with integer coordinates. You are asked to compute the smallest perimeter of a triangle with distinct vertexes from this set of points.
Input file format
The first line contains one integer N — number of points.
Each of the next N lines contains two integer numbers xi, yi — coordinates of i-th point.
Output file format
Output file should contain one real number — the minimum perimeter. Answers with a relative or absolute error of at most 10−7 will be considered correct. Degenerate triangles -— triangles with zero area -— are ok.
Constraints
0 ≤ n ≤ 106
0 ≤ xi, yi ≤ 109


