Задача A. Поездка на Хэллоуин
Условие
Владивостокский программист приглашает коллегу к себе домой в гости на празднование Хэллоуина.
Оба программиста живут за городом.
Их дома расположены в точках с координатами (XA; YA) и (XB; YB).
В этом районе есть только одна асфальтированная дорога, представимая в виде отрезка с координатами
начала (XS; YS) и конца (XE; YE). Дорога является платной: за
любой въезд на дорогу (проезд по произвольному участку дороги или только пересечение —
не имеет значения) взимается плата в размере CR.
Остальная местность занята полями, которые
(в связи со скорым Хэллоуином) сплошь засажены тыквами.
При движении на автомобиле по полю взимается
плата в размере CF за каждый километр пути — ущерб за раздавленные тыквы.
Помогите программисту добраться к другу с минимальными затратами.
Обратите внимание, при сколь угодно малом приближении к дороге плата за въезд на неё не взимается.
Смотрите пример №3.
Формат входного файла
Во входном файле содержатся десять целых чисел:
XA YA XB YB XS YS XE YE CF CR
Формат выходного файла
Выходной файл должен содержать единственное число —
минимальные затраты при перемещении из
A в
B с абсолютной ошибкой не более
10−3.
Ограничения
−103 ≤ XA, YA, XB, YB, XS, YS, XE, YE ≤ 103
1 ≤ CF ≤ 103
1 ≤ CR ≤ 106
Дома программистов находятся в разных точках и не находятся на дороге
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
1 1 2 2 0 3 3 0 1 1
|
2.414213562373095
|
| 2 |
1 5 4 0
-2 -2 10 10
1 2
|
7.656854249492381
|
| 3 |
10 10 25 19
15 13 20 16
1 1000000
|
17.492855684535900
|
Задача B. Пеленг НЛО
Условие
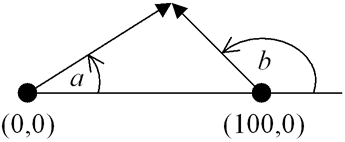
Два радара, расположенные в точках с координатами (0, 0) и (100, 0),
обнаружили неопознанный объект.
По таинственной причине, связанной, возможно, с внеземной природой объекта,
радары оказались способны определить только направление на объект (пеленг),
но не расстояние до объекта.
Пеленг измеряется в градусах, против часовой стрелки,
начиная от направления "на восток"
(т. е. пеленг второго радара относительно первого равен 0°,
пеленг первого радара относительно второго — 180°).
Требуется найти координаты НЛО или определить, что это невозможно.
Формат входного файла
Во входном файле содержатся вещественные числа
a и
b, разделенные пробелами.
Формат выходного файла
В выходном файле должны содержаться два вещественных числа,
x и
y,
представляющие координаты объекта с точностью до 4 знаков после запятой.
Если определить координаты невозможно, следует вывести два числа
0 (нуль).
Ограничения
0 ≤ a, b ≤ 360
Примеры тестов
| № |
Входной файл (input.txt) |
Выходной файл (output.txt) |
|---|
| 1 |
45.1 135.0
|
49.9127 50.0873
|
| 2 |
135.0 45.0
|
0 0
|
Problem C. Circular Area
Statement
Your task is to write a program, which, given two circles,
calculates the area of their intersection with the accuracy of two
digits after decimal point.
Input file format
In the single line of input file there are space-separated real numbers
x1 y1 r1 x2 y2 r2.
They represent center coordinates and radii of two circles.
Output file format
The output file must contain single real number — the area.
Sample tests
| No. |
Input file (input.txt) |
Output file (output.txt) |
|---|
| 1 |
20.0 30.0 15.0 40.0 30.0 30.0
|
608.37
|
Problem D. Area 51
Statement
Michael and Nick are living near the famous top-secret Area 51 facility.
The facility is enclosed by a fence and is so large that for
the purpose of this problem we consider the fence being a line
that stretches infinitely into both directions.
Only extremely brave boys are not scared to go to the fence
and peek at the facility. Nick is among the brave ones.
He once came to the fence and saw a number of chimneys with distinct shapes.
As a proof of his bravery he tells everybody what chimneys
he saw from his left to his right.
Michael’s father is working at Area51”and has a facility’s map at his home.
Michael found this map and he can now verify Nick's claim of being near
the facility's fence. However, it turns out to be complicated,
and your task is to write a program to perform this verification.
On a map distinctly shaped chimneys are denoted by capital
letters from A to Z.
Each letter denotes a distinct shape, but chimneys with this shape
can appear more than once on a map. The map uses Cartesian coordinate
system oriented so that the fence is Ox axis and all chimneys are
located on a half-plane with a positive y coordinate.
All chimneys are considered to be points (their sizes and actual
geometrical shapes are ignored for the purpose of this problem).
Nick claims that he looked from a point on the fence where
no two chimneys were on the same line of his
sight (a line that originates from his point of view).
It means that at the point he looked from, all the
chimneys he saw had a well-defined order from left to right.
Michael have already made a preliminary verification of Nick's claim.
He made sure that the number of distinctly shaped chimneys matches
their number on the map. Now Michael needs to perform a final
verification to get a list of x coordinates on a fence (if any)
where the corresponding arrangement of chimneys could be seen from.
This information shall be presented as an ordered list of open intervals
(a1, b1), (a2, b2), …, (an, bn), so that
a1 < b1 ≤ a2 < b2 ≤ … ≤ an < bn.
Asterisk symbol ("*") is used in place of a1 and/or bn to denote
interval that extends to infinity on the left or on the right
correspondingly.
Note, that bi = ai+1 = x in case where Nick
could not have been at the point x on a fence, because he
would have seen more than one chimney on a single line of his sight,
but being to the left or to the right
of x yields the order of chimneys that he saw.
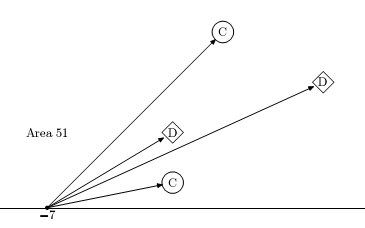
The picture below shows that if the boy looks
from the point x = −7 he sees the chimneys in the following
order: C, D, D, C.
It is so for any point from the set
(−∞,−11) ∪ (−11,−3.5) ∪ (14,+∞) — the first
example from the problem statement.
Input file format
The first line of the input file contains an integer number
m
the number of chimneys at the "Area 51" facility.
The second line of the input file contains a string
of
m letters from A to Z that describe the chimneys that Nick
saw from his left to his right. A single letter can be used more than
once (if Nick saw the same shape more than once).
Then follow
m lines that describe chimneys on the map.
Each line contains three tokens separated by spaces — chimney shape letter
(from A to Z), and two integers
xi and
yi — chimney coordinates.
On these
m lines letters appear in arbitrary order,
but each letter from A to Z appears
the same number of times as on the second line of the input file.
No two chimneys have the same coordinates.
Output file format
Write to the first line of the output file a single integer number
n —
the number of intervals that describe
x coordinates on a fence
where Nick could have seen the corresponding arrangement of chimneys from.
Write to the second line of the output file
2 n numbers
a1, b1, …, an, bn using "*" instead of a number
a1 and/or
bn to denote infinity.
Numbers must be precise up to
10−6.
Constraints
1 ≤ m ≤ 100,
−100 ≤ xi ≤ 100,
0 < yi ≤ 100
Sample tests
| No. |
Input file (area.in) |
Output file (area.out) |
|---|
| 1 |
4
CDDC
C 0 7
D 4 5
C -2 1
D -2 3
|
3
* -11 -11 -3.5 14 *
|
| 2 |
4
DCCD
C 0 7
D 4 5
C -2 1
D -2 3
|
2
-3.5 -2.333333 -2.333333 -2
|
| 3 |
4
DCDC
C 0 7
D 4 5
C -2 1
D -2 3
|
0
|

