Летний турнир 2016 - Лена и зеркало

Задача D. Лена и зеркало ≡

задачи
видимые пробелы
простые формулы
широкий текст
редактор

Автор:	Г. Гренкин	Ограничение времени:	1 сек
Входной файл:	input.txt	Ограничение памяти:	256 Мб
Выходной файл:	output.txt

Условие

Лена любит смотреть в зеркало. Она любит не только смотреть на своё отражение, но и изучать законы оптики, наблюдая за ходом световых лучей.

Так как Солнце находится на достаточно большом расстоянии от Земли, при расчётах часто считают Солнце бесконечно удалённой точкой. В этом случае световые лучи, испускаемые Солнцем, считают параллельными друг другу.

В определённый день и в определённый момент времени Солнце находится в определённом месте. Соответственно, солнечные лучи падают туда, где находится Лена, под определённым углом. Лена, в свою очередь, может наклонять зеркало под разными углами.

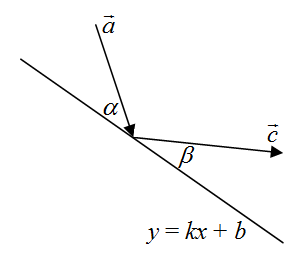
Пусть зеркало наклонено так, что в некоторой системе координат его можно задать как прямую, имеющую уравнение $y = kx + b$ . Направление падения солнечных лучей задаётся единичным вектором $a$ .

Требуется найти направление отражения лучей, а именно, требуется найти единичный вектор $c$ .

Примечание. По законам оптики, свет отражается так, что угол падения равен углу отражения (α = β на рисунке).

Формат входного файла

Входной файл содержит три вещественных числа $k\,x_1\,y_1$ — угловой коэффициент прямой и координаты вектора $a$ .

Длина вектора $a$ приближённо равна $1$ .

Формат выходного файла

Выходной файл должен содержать два вещественных числа $x_2\,y_2$ — координаты вектора $c$ .

Длина вектора $c$ должна быть приближённо равна $1$ .

Координаты вектора $c$ должны быть выведены с точностью до 3-х знаков после запятой.

Ограничения

$-1000 \le k \le 1000$

Примеры тестов

№	Входной файл (`input.txt`)	Выходной файл (`output.txt`)
1	`0 0.7071067812 -0.7071067812`	`0.7071067812 0.7071067812`
2	`1 1 0`	`0 1`

Разбор

Пусть $l$ — единичный направляющий вектор прямой, $n$ — единичный вектор нормали к прямой. Эти векторы перпендикулярны друг другу.

Рассмотрим базис, состоящий из векторов $l$ и $n$ . Разложим вектор $a$ по этому базису: $a$ $= N$ $n$ $+ L$ $l$ .

Тогда вектор $c$ можно найти по формуле: $c$ $= -N$ $n$ $+ L$ $l$ $= 2L$ $l$ $-$ $a$ .

Так как базис { $n$ , $l$ } ортогональный (т.е. векторы базиса перпендикулярны друг другу) и векторы базиса единичные, координату $L$ можно найти по формуле: $L =$ $a$ · $l$ .

Следовательно, $c$ $= 2($ $a$ · $l$ $)$ $l$ $-$ $a$ .

Найдём направляющий вектор. Выберем на прямой две точки: $A(0,\,b)$ и $B(1,\,k + b)$ . Тогда в качестве направляющего вектора можно взять вектор $AB$ { $1,\,k$ }. Единичный направляющий вектор: $l$ { $1/\sqrt{k^2 + 1},\,k/\sqrt{k^2 + 1}$ }.