Problem G. Group performance ≡
| Author: | I. Tufanov | Time limit: | 3 sec | |
| Input file: | input.txt | Memory limit: | 256 Mb | |
| Output file: | output.txt |
Statement
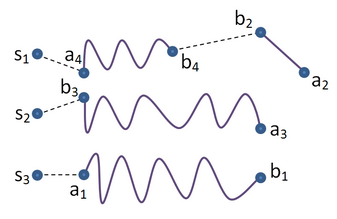 Multi-vehicle cooperation is a hot topic in contemporary underwater robotics.
Often a group of vehicles can finish the mission faster than just one.
But you have to implement sophisticated control techniques to benefit from the cooperation.
Multi-vehicle cooperation is a hot topic in contemporary underwater robotics.
Often a group of vehicles can finish the mission faster than just one.
But you have to implement sophisticated control techniques to benefit from the cooperation.
Consider N vehicles and M tasks they should accomplish. Each task should be accomplished by exactly one vehicle. Each task is a track that a vehicle should follow. The task number i is defined by two edge points ai and bi, and length di (di ≥ |ai − bi|).
Vehicle is allowed to follow a track in any direction — either from ai to bi or from bi to ai. In both cases the length of the path will be di.
A plan is a sequence of tasks for each vehicle in order of execution. Every task in the plan is followed either in direct order (a to b) or in reverse order (from b to a). Each task should appear exactly once in the whole plan.
The j-th vehicle has a starting point sj. Vehicle executes its tasks according to its part of a plan. When a vehicle accomplishes one task, it goes to the start point of the next one, moving along the straight line. When all tasks assigned to a vehicle are done, it stops. Vehicle path length is a total path traveled by the vehicle during the plan execution. Plan length is a maximal vehicle path length of all vehicles in the plan.
Your program must, given vehicles and tasks, find a plan of minimal length.
Assume that vehicles operate on a plane (plane of constant depth) and that the vehicle size may be ignored.
Input file format
Each point in the input file is described with two integers — its x and y coordinates.
On the first line of input file there are integers N M. Following N lines describe starting points si.
Next M lines describe tasks, each task descriptions consisting of points ai, bi and path length di.
Output file format
Output file must describe a plan of minimal length. If there several such plans, output any of them.
Plan description consists of N blocks, each describes a sequence of tasks for one vehicle. j − th block starts with non-negative integer numj, followed by numj pairs (tjk, dirjk). Here tjk denotes a number of k-th task for j-th vehicle, it is an integer in range 1..M. The dirjk is either 0 or 1: 0 stands for passing tjk from a to b, 1 stands for passing tjk from b to a.
Constraints
1 ≤ N, M ≤ 10; 0 ≤ di ≤ 104;
All coordinates are integers in range 0..103.
Sample tests
| No. | Input file (input.txt) |
Output file (output.txt) |
|---|---|---|
| 1 | |
|