Problem B. Bearded joke ≡
| Author: | Антон Карабанов | Time limit: | 1 sec | |
| Input file: | Standard input | Memory limit: | 256 Mb | |
| Output file: | Standard output |
Statement
Some kind of an old joke: Letter to the Balabanovo Match Factory. "I constantly count the matches in your boxes — they are 59, then 60, and sometimes 58. Are you all crazy there or something???"
Obsessed pensioner Oderyozhimov made another control purchase of k ? 2 boxes of matches. His fears were confirmed—all the boxes contained a different number of matches, and again they turned out to be consecutive natural numbers. The old man admired the beautiful equilateral triangle folded from all the matches with a side of n, divided into unit triangles, and began his next letter.
Input format
The only line of input contains a natural number: n — the side of the triangle.
Output format
Output a single natural number — the number of different suitable values for k.
Constraints
1 ≤ n ≤ 500000
Example explanation
In the example, n = 4 is given (see the picture). In the resulting figure, exactly 30 matches.
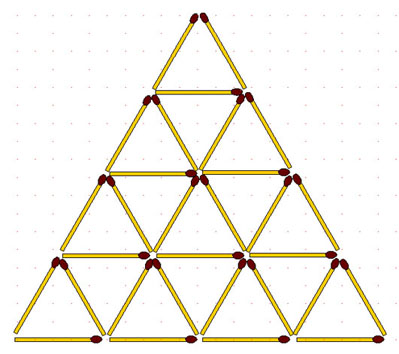
The pensioner could buy three boxes with 9, 10, and 11 matches.
He could buy four boxes with 6, 7, 8, and 9 matches.
Or he could buy five boxes with 4, 5, 6, 7, and 8 matches.
There are no other suitable solutions.
Sample tests
| No. | Standard input | Standard output |
|---|---|---|
| 1 | |
|
Explanation
Треугольник содержит 3 * n * (n + 1) // 2 спичек.
Пусть куплено k коробков, в которых содержалось a + a+1 + a+2 + ... + a+k-1 = a*k + (1 + 2 + ... + k-1) = a*k + k*(k-1) // 2 спичек.
Тогда можно перебрать k от 2 до k * (k-1) // 2, что не больше 3 * n * (n + 1) // 2 и попробовать вычислить подходящее a.