Problem G. Guards ≡
| Author: | NEERC 2005 | Time limit: | 2 sec | |
| Input file: | guards.in | Memory limit: | 64 Mb | |
| Output file: | guards.out |
Statement
Agency of Criminal Matters (ACM) provides protection for corporate offices. The agency employs security guards that work in 12 hours shifts. Every 24 hours day consists of a 12 hours daylight shift and 12 hours nighttime shift (day starts with a daylight shift). Security guards are hired to work on different schedules. Some schedules are simply periodic (certain pattern repeats in a specified number of days), while others are weekly (with a standard 7 days week) or depend on the day of the week. For this purpose Monday through Friday are considered to be workdays; Saturday and Sunday are considered to be weekends. Each security guard works on one of the following four schedules:
1. Day of work (daylight and nighttime shifts) and two days (daylight and nighttime) of rest - work every third day.
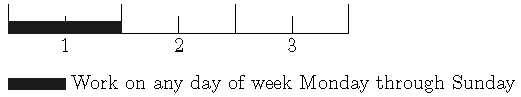
2. Only daylight shifts on 5 workdays of a week (no work in nighttime and weekends).
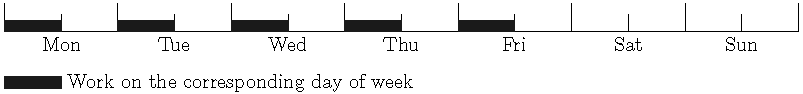
3. Day of work (daylight and nighttime), day of rest (daylight and nighttime), daylight shift of work, nighttime of rest, and one more day (daylight and nighttime) of rest — 3 shifts of work every 4 days.
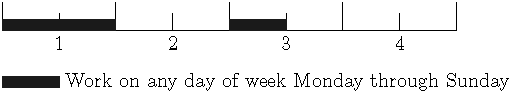
4. Day of work (daylight and nighttime), day of rest (daylight and nighttime), day of work only during daylight (rest during nighttime), day of work (daylight and nighttime), day of rest (daylight and nighttime); but if any daylight shift falls on the weekend then it is cancelled — 3 daylight shifts and 2 nighttime shifts every 5 days with the exception of weekends (where only nighttime shifts are possible).

ACM has to provide protection for a location based on the following requirements. There has to be at least a certain number of guards during daylight shifts on workdays, at least a certain number of guards during daylight shifts on weekends, and at least a certain number of guards during nighttime shifts (it does not matter whether it is a workday or a weekend).
As an additional requirement (for simplicity of planning) the schedule of protection for every location has to be regular. In a regular schedule there is a fixed number of guards that work on any particular schedule during every daylight workday shift, nighttime workday shift, daylight weekend shift, and nighttime weekend shift. For example, if 4 guards on the 1st schedule work on some daylight workday shift, then 4 guards on the 1st schedule work on all daylight workday shifts (they might be different persons, though). Your task is to determine the minimal number of guards that have to be hired for protection of the specific location given its requirements.
Input file format
The input file consists of a line with three integer numbers — n1, n2, and n3. Here n1 is the minimum required number of guards during daylight shifts on workdays, n2 is the minimum required number of guards during daylight shifts on weekends, and n3 is the minimum required number of guards during nighttime shifts.Output file format
Write to the output file a single line with four integer numbers — m1, m2, m3, and m4. Here mi is the number of security guards working on i-th schedule that are needed to establish security of a location with the given requirements. You have to write an answer that requires minimal number of guards in total, choosing any answer among those.Constraints
1 ≤ n1, n2, n3 ≤ 1000Sample tests
| No. | Input file (guards.in) |
Output file (guards.out) |
|---|---|---|
| 1 | |
|
| 2 | |
|